

解析:盒子的体积y和以x为自变量的函数解析式为y=(30-2x)2x.
如果要做成一个容积是1 200 cm3的无盖盒子,那么有方程(30-2x)2x=1 200,其定义域为{x|0<x<15}.
令f(x)=(30-2x)2x-1 200,借助计算机画出函数图象.由图象可以看出,函数f(x)分别在区间(1,2)和(9,10)内各有一个零点,即方程(30-2x)2x=1 200分别在区间(1,2)和(9,10)内各有一个解.下面用二分法求方程的近似解.
取区间(1,2)的中点x1=1.5,用计算器算得f(1.5)=-106.5<0.
因为f(1.5)·f(2)<0,所以x0∈(1.5,2).
同理可得x0∈(1.5,1.75),x0∈(1.625,1.75),x0∈(1.687 5,1.75),x0∈(1.687 5,1.718 75),x0∈(1.687 5,1.703 125),x0∈(1.687 5,1.695 312 5).
由于|1.695 312 5-1.687 5|=0.007 812 5<0.1,
此时区间(1.687 5,1.695 312 5)的两个端点精确至0.1的近似值都是1.7,所以方程在区间(1,2)内精确到0.1的近似解为1.7.同理可得方程在区间(9,10)内精确到0.1的解为9.4.
故如果要做成一个容积是1 200cm3的无盖盒子,截去的小正方形的边长大约是1.7 cm或9.4 cm.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:中学教材全解 高中数学 必修1(人教A版) 人教A版 题型:044
如图,有一块边长为15 cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
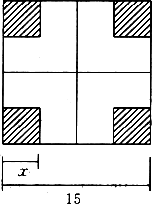
(1)求出盒子的体积y以x为自变量的函数解析式,并讨论这个函数的定义域;
(2)如果要做一个容积是150 cm3的无盖盒子,那么截去的小正方形的边长x是多少(精确到0.1 cm)?
查看答案和解析>>
科目:高中数学 来源:志鸿系列训练必修一数学北师版 题型:044
如图,有一块边长为15 cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.

(1)求出盒子的体积y以x为自变量的函数解析式,并讨论这个函数的定义域;
(2)如果要做成一个容积是150 cm3的无盖盒子,那么截去的小正方形的边长x是多少厘米(精确到0.1 cm)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com