设数列{an}的前n项的和为Sn,满足Sn+an=n+3(n∈N*).
(1)求证:存在常数c,使数列{an+c}是等比数列;
(2)求an与Sn;
(3)设Tn=Sn-nan(n∈N*),求证:Tn+1>Tn.
解:(1)证明:S
n+a
n=n+3①;S
n-1+a
n-1=n+2 ②
①式与②式相减,得 2a
n-a
n-1=1,经过变形,得
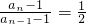
,
显然存在常数c=-1,使得数列{a
n-1}是等比数列,且公比q=

(2)当n=1,有s
1+a
1=2a
1=1+3,可得a
1=2,
由{a
n-1}是等比数列,公比q=0.5,当n>1时,可知a
n-1=(a
1-1)q
n-1化简,得a
n=0.5
n-1+1
s
n=n+3-an=n+2-q^(n-1)=n+2-0.5
n-1
(3)证明:T
n+1=S
n+1-(n+1)×a
n+1=s
n-na
n+1 由T
n=S
n-na
n,两式相减,得T
n+1-T
n=n[a
n-a
n+1]③
由于n为N正,n>0,当n=1时,a
n=2,a
n+1=1,a
n-a
n+1>0,故③式右边大于0,故T
n+1>T
n.
当n>1时,由前面得a
n-a
n+1=0.5a
n>0,故③式右边大于0,故T
n+1>T
n.
得证
分析:(1)写出S
n-1+a
n-1=n+2与条件相减,经过整理变形,从而可构造新数列得证;
(2)由(1){a
n-1}是等比数列,且公比q=

,可求通项,进而可以求S
n;
(3)先由条件得T
n+1=S
n+1-(n+1)×a
n+1=s
n-na
n+1再与条件相减得T
n+1-T
n=n[a
n-a
n+1],从而可证.
点评:本题主要考查构造法求新数列,考查数列的通项与前n项和,多次使用两式相减得方法,属于中档题.

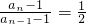 ,
,
 ,可求通项,进而可以求Sn;
,可求通项,进而可以求Sn;
