
 如图四棱椎P-ABCD中,四边形ABCD是矩形,平面PAD⊥平面ABCD,其中M,N分别是PD,BC的中点
如图四棱椎P-ABCD中,四边形ABCD是矩形,平面PAD⊥平面ABCD,其中M,N分别是PD,BC的中点分析 (Ⅰ)推导出BA⊥AD,由此利用平面PAD⊥平面ABCD,能证明BA⊥平面PAD.
(Ⅱ)取PA中点E,连结ME,BE,推导出四边形ABCD是矩形,从而四边形BNME是平行四边形,进而MN∥BE,由此能证明MN∥平面PAB.
解答 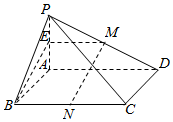 证明:(Ⅰ)∵四边形ABCD是矩形,∴BA⊥AD,
证明:(Ⅰ)∵四边形ABCD是矩形,∴BA⊥AD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BA⊥平面PAD.
解:(Ⅱ)取PA中点E,连结ME,BE,
∵M,E分别是PA,PD中点,
∴在△PAD中,EM$\underset{∥}{=}$$\frac{1}{2}$AD,
又N是BC中点,四边形ABCD是矩形,
∴BN$\underset{∥}{=}$$\frac{1}{2}$AD,∴BN$\underset{∥}{=}$EM,
∴四边形BNME是平行四边形,
∴MN∥BE,
又BE?平面PAB,MN?平面PAB,
∴MN∥平面PAB.
点评 本题考查线面垂直的证明,考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
 如图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第第14次的考试成绩依次记为A1,A2,…A14,如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,那么算法流程图输出的结果是( )
如图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第第14次的考试成绩依次记为A1,A2,…A14,如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,那么算法流程图输出的结果是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{2}$ | B. | $\frac{35}{2}$ | C. | 14 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{5}^{3}$($\frac{1}{4}$)3($\frac{3}{4}$)2 | B. | C${\;}_{5}^{3}$($\frac{1}{4}$)2($\frac{3}{4}$)3 | C. | C${\;}_{4}^{2}$($\frac{1}{4}$)3($\frac{3}{4}$)2 | D. | C${\;}_{4}^{2}$($\frac{1}{4}$)2($\frac{3}{4}$)3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com