Question

16．$\overrightarrow a=（\sqrt{3}sin2x，cos2x），\overrightarrow b=（cos2x，-cos2x），f（x）=\overrightarrow a•\overrightarrow b+\frac{1}{2}$．
（1）若$x∈（\frac{7}{24}π，\frac{5}{12}π）$时，$\overrightarrow a•\overrightarrow b+\frac{1}{2}=-\frac{3}{5}$，求cos4x的值；
（2）将$f（x）=\overrightarrow a•\overrightarrow b+\frac{1}{2}$的图象向左移$\frac{π}{8}$，再将各点横坐标伸长为原来的2倍，纵坐标不变，得y=g（x），若关于g（x）+m=0在区间$[0，\frac{π}{2}]$上的有且只有一个实数解，求m的范围．

Answer 1

分析 （1）由题意，根据平面向量的数量积运算求出cos（4x+$\frac{π}{3}$）的值，再利用三角恒等变换求出cos4x的值；
（2）由（1）知f（x）的解析式，利用图象平移和变换得出g（x）的解析式，画出函数g（x）的图象，结合图象求出m的取值范围．

解答 解：（1）$\overrightarrow{a}$=（$\sqrt{3}$sin2x，cos2x），$\overrightarrow{b}$=（cos2x，-cos2x），
∴f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{1}{2}$
=$\sqrt{3}$sin2xcos2x-cos²2x+$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin4x-$\frac{1}{2}$cos4x-$\frac{1}{2}$+$\frac{1}{2}$
=-cos（4x+$\frac{π}{3}$）=-$\frac{3}{5}$，
∴cos（4x+$\frac{π}{3}$）=$\frac{3}{5}$；
又$x∈（\frac{7}{24}π，\frac{5}{12}π）$时，4x+$\frac{π}{3}$∈（$\frac{3π}{2}$，2π），
∴sin（4x+$\frac{π}{3}$）=-$\sqrt{1{-（\frac{3}{5}）}^{2}}$=-$\frac{4}{5}$，
∴cos4x=cos[（4x+$\frac{π}{3}$）-$\frac{π}{3}$]
=cos（4x+$\frac{π}{3}$）cos$\frac{π}{3}$+sin（4x+$\frac{π}{3}$）sin$\frac{π}{3}$
=$\frac{3}{5}$×$\frac{1}{2}$+（-$\frac{4}{5}$）×$\frac{\sqrt{3}}{2}$
=$\frac{3-4\sqrt{3}}{10}$；
（2）由（1）知，f（x）=$\frac{\sqrt{3}}{2}$sin4x-$\frac{1}{2}$cos4x=sin（4x-$\frac{π}{6}$），
将f（x）的图象向左平移$\frac{π}{8}$个单位，得y=sin[4（x+$\frac{π}{8}$）-$\frac{π}{6}$]=sin（4x+$\frac{π}{3}$）的图象；
再将y各点横坐标伸长为原来的2倍，纵坐标不变，得y=sin（2x+$\frac{π}{3}$）的图象；
则y=g（x）=sin（2x+$\frac{π}{3}$）；
当x∈$[0，\frac{π}{2}]$时，2x+$\frac{π}{3}$∈[$\frac{π}{3}$，$\frac{4π}{3}$]，
画出函数g（x）的图象，如图所示；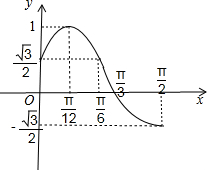

则g（x）+m=0在区间$[0，\frac{π}{2}]$上的有且只有一个实数解时，
应满足-$\frac{\sqrt{3}}{2}$≤-m＜$\frac{\sqrt{3}}{2}$或-m=1；
即-$\frac{\sqrt{3}}{2}$＜m≤$\frac{\sqrt{3}}{2}$，或m=-1．

点评 本题考查了三角函数的图象与性质的应用问题，也考查了平面向量数量积的运算问题，是综合题．