
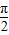 ],f(x)≥kx总成立,求实数k的取值范围;
],f(x)≥kx总成立,求实数k的取值范围;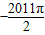 ,
,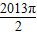 ].过点M(
].过点M(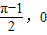 )作函数F(x)图象的所有切线,令各切点的横坐标构成数列{xn},求数列{xn}的所有项之和S的值.
)作函数F(x)图象的所有切线,令各切点的横坐标构成数列{xn},求数列{xn}的所有项之和S的值.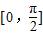 时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;
时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;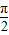 对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.
对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.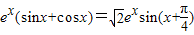 .
.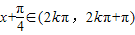 ,即
,即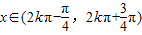 时,f′(x)>0;
时,f′(x)>0;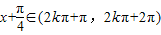 ,即
,即 时,f′(x)<0.
时,f′(x)<0.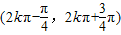 (k∈Z),
(k∈Z),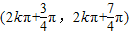 (k∈Z).
(k∈Z).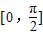 时g(x)min≥0.
时g(x)min≥0.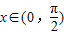 )
)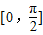 上为增函数,所以
上为增函数,所以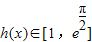 .
.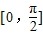 上为增函数,所以g(x)min=g(0)=0,
上为增函数,所以g(x)min=g(0)=0,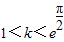 时,g′(x)=0在上有实根x,因为h(x)在
时,g′(x)=0在上有实根x,因为h(x)在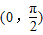 上为增函数,
上为增函数,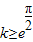 时,g′(x)≤0恒成立,所以g(x)在
时,g′(x)≤0恒成立,所以g(x)在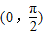 上为减函数,
上为减函数,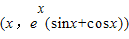 ,则斜率为
,则斜率为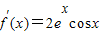 ,
,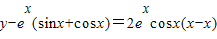 ,
,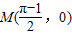 的坐标代入切线方程,得
的坐标代入切线方程,得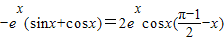
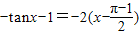 ,即
,即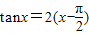 ,
,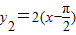 ,则这两个函数的图象均关于点
,则这两个函数的图象均关于点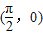 对称,
对称,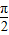 对称成对出现,
对称成对出现,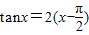 x∈
x∈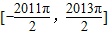 的根,
的根,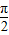 对称成对出现,
对称成对出现,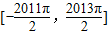 内共构成1006对,每对的和为π,
内共构成1006对,每对的和为π,

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com