
| A. | 5海里 | B. | $5(\sqrt{3}-1)$海里 | C. | 10海里 | D. | $10(\sqrt{3}-1)$海里 |
分析 依题意画出图形,得到∠BAC=45°,∠BAD=75°,所以∠CAD=∠CDA=30°,CD10,在三角形ADC中,利用正弦定理,能求出这艘船的速度.
解答 解:如图,依题意有∠BAC=45°,∠BAD=75°,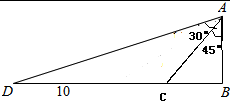 所以∠CAD=∠CDA=30°,
所以∠CAD=∠CDA=30°,
从而CD=10,设船的速度为x海里/小时,则BC=$\frac{x}{2}$,AC=$\frac{\sqrt{2}}{2}x$,
在三角形ADC中,得AC=$\frac{\sqrt{2}}{2}$x,CD=10,∠D=15°,所以$\frac{\frac{\sqrt{2}}{2}x}{sin15°}=\frac{10}{sin30°}$,解得x=10($\sqrt{3}$-1);
于是这艘船的速度是10($\sqrt{3}$-1)海里/小时.
故选D
点评 本题考查三角形知识的实际运用,解题时要注意数形结合思想的灵活运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{80}{883}$ | C. | $\frac{1}{12}$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S?T | B. | T?S | C. | S=T | D. | S∩T=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-8)2+(y-3)2=25 | B. | (x-8)2+(y+3)2=5 | C. | (x-8)2+(y-3)2=5 | D. | (x-8)2+(y+3)2=25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com