
如下图(1)、(2)、(3)、(4)四个图案,每个图案都是由小正方形拼成,现按同样的规律 (小正方形的摆放规律相同)进行拼图,设第n个图形包含f(n)个小正方形.

(1)f(6)= ;
(2) f(n)= .
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
某工厂的一、二、三车间在12月份共生产了3 600双皮靴,在出厂前要检查这批产品的质量,决定采用分层抽样的方法进行抽取,若从一、二、三车间抽取的产品数分别为a、b、c,且a、b、c构成等差数列,则二车间生产的产品数为( )
A.800 B.1 000 C.1 200 D.1 500
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆 的圆心为
的圆心为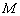 ,
, 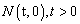 且
且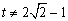 ,设
,设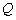 为圆上任一点,线段
为圆上任一点,线段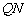 的垂直平分线交直线
的垂直平分线交直线 于点
于点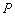 .
.
(1)试讨论动点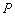 的轨迹类型;
的轨迹类型;
(2)当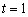 时,设动点
时,设动点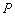 的轨迹为曲线
的轨迹为曲线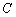 ,过
,过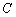 上任一点
上任一点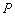 作直线
作直线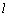 ,
,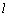 与曲线
与曲线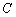 有且只有一个交点,
有且只有一个交点,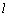 与圆
与圆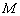 交于点
交于点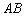 ,若
,若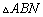 的面积是
的面积是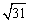 ,求直线
,求直线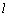 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
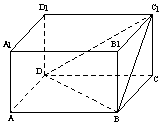
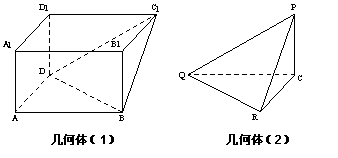
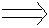
如图,在长方体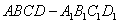 中,
中,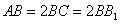 , 沿平面
, 沿平面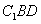 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)
(I)设几何体(1)、几何体(2)的体积分为是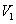 、
、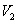 ,求
,求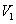 与
与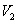 的比值
的比值
(II)在几何体(2)中,求二面角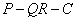 的正切值
的正切值
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com