
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 利用正弦定理以及两角和的正弦函数求出A的值,通过内角和化简所求表达式为B的三角函数,然后求出表达式的最大值.
解答 解:由asinB=bcosA以及正弦定理可知sinAsinB=sinBcosA,⇒A=$\frac{π}{4}$,
∴$2sinB-\sqrt{2}cosC$
=2sinB-$\sqrt{2}$cos($\frac{3π}{4}$-B)
=2sinB-$\sqrt{2}$(cos$\frac{3π}{4}$cosB+sin$\frac{3π}{4}$sinB)
=2sinB+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$cosB-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$sinB
=2sinB+cosB-sinB
=$\sqrt{2}$sin($\frac{π}{4}$+B).
∴$2sinB-\sqrt{2}cosC$的最大值为$\sqrt{2}$.
故选:A.
点评 本题考查正弦定理的应用,三角函数中的恒等变换的应用,考查计算能力.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cb2<ab2 | B. | ab<ac | C. | c(a-c)>0 | D. | a+ac>b+ac |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
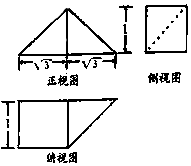 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )| A. | $4+3\sqrt{3}$ | B. | $3+3\sqrt{3}$ | C. | $4+2\sqrt{3}$ | D. | $3+4\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com