
分析 ①利用数列递推关系、等差数列的通项公式即可得出.
②利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:①$4{S_n}={({a_n}+1)^2}$,
$4{S_{n-1}}={({a_{n-1}}+1)^2}$n≥2,
相减可得:$4{a_n}={a_n}^2-{a_{n-1}}^2+2{a_n}-2{a_{n-1}}$(an+an-1)(an-an-1-2)=0,n≥2…(2分)
∵an>0,an+an-1>0,
∴an=an-1+2…(4分)
又$4{S_1}=4{a_1}={({a_1}+1)^2}$
即a1=1…(5分)
∴an=2n-1…(6分)
②${b_n}=(2n-1)•{(\frac{1}{3})^n}$,
${T_n}=1•\frac{1}{3}+3•{(\frac{1}{3})^2}+5•{(\frac{1}{3})^3}+…+(2n-1)•{(\frac{1}{3})^n}$,$\frac{1}{3}{T_n}=1•{(\frac{1}{3})^2}+3•{(\frac{1}{3})^3}+…+(2n-3)•{(\frac{1}{3})^n}+(2n-1)•{(\frac{1}{3})^{n+1}}$,
相减$\frac{2}{3}{T_n}=\frac{1}{3}+2•{(\frac{1}{3})^2}+2•{(\frac{1}{3})^3}+…+2•{(\frac{1}{3})^n}-(2n-1)•{(\frac{1}{3})^{n+1}}$
=$2×\frac{{\frac{1}{3}-{{(\frac{1}{3})}^{n+1}}}}{{1-\frac{1}{3}}}-\frac{1}{3}-(2n-1)•{(\frac{1}{3})^{n+1}}$=$\frac{2}{3}-\frac{2(n+1)}{3}•{(\frac{1}{3})^n}$…(10分)
∴${T_n}=1-(n+1)•\frac{1}{3^n}$…(12分)
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $7+\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $\sqrt{46}+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
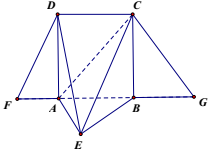 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com