
| A. | $7+\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $\sqrt{46}+\sqrt{2}$ |
分析 判断椭圆与圆的位置关系,设出P的参数坐标,求解P与圆的圆心的距离的最大值,然后求解P,Q两点间的最大距离.
解答 解:由题意可知椭圆$\frac{x^2}{10}+{y^2}=1$长半轴为:$\sqrt{10}$,和圆x2+(y-6)2=2圆心是C(0,6)半径为$\sqrt{2}$相离,
P为椭圆$\frac{x^2}{10}+{y^2}=1$上的点($\sqrt{10}$cosθ,sinθ),Q是圆x2+(y-6)2=2上的点,
|PC|=$\sqrt{10co{s}^{2}θ+(sinθ-6)^{2}}$=$\sqrt{9co{s}^{2}θ-12sinθ+37}$
=$\sqrt{46-9si{n}^{2}θ-12sinθ}$=$\sqrt{50-(3sinθ+2)^{2}}$≤5$\sqrt{2}$,
则P,Q两点间的最大距离是:$\sqrt{2}+5\sqrt{2}$=$6\sqrt{2}$.
故选:B.
点评 本题考查椭圆的简单性质以及参数方程的应用,椭圆与圆的位置关系的应用,考查分析问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+1,x∈[-2,2) | B. | f(x)=|3x-1|-|3x+1| | ||
| C. | f(x)=-x2+1,x∈(-2,+∞) | D. | f(x)=x4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
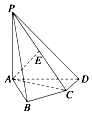 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉[1,2],x2-4x+6≥0 | B. | ?x0∈[1,2],x02-4x0+6≥0 | ||
| C. | ?x∉[1,2],x2-4x+6>0 | D. | ?x∈[1,2],x2-4x+6≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com