
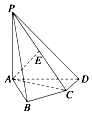
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.分析 (1)证明:CD⊥平面PAC,可得AE⊥CD,证明AE⊥PC,即可证明AE⊥平面PCD;
(2)证明∠APB为PB和平面PAD所成的角,即可求PB和平面PAD所成的角的大小.
解答 (1)证明:在四棱锥P-ABCD中,因为PA⊥底面ABCD,CD?平面ABCD,
故CD⊥PA.…(1分)
由条件CD⊥AC,PA∩AC=A,…(2分)
∴CD⊥平面PAC.…(3分)
又AE?平面PAC,∴AE⊥CD.…(4分)
由PA=AB=BC,∠ABC=60°,可得AC=PA.…(5分)
∵E是PC的中点,∴AE⊥PC.…(6分)
又PC∩CD=C,
综上得AE⊥平面PCD.…(7分)
(2)解:在四棱锥P-ABCD中,因为PA⊥底面ABCD,AB?平面ABCD,故PA⊥AB.…(8分)
又AB⊥AD,PA∩AD=A,则 AB⊥平面PAD,…(9分)
故PB在平面PAD内的射影为PA,则∠APB为PB和平面PAD所成的角.…(10分)
在Rt△PAB中,AB=PA,
故∠APB=45°.…(11分)
所以PB和平面PAD所成的角的大小为45°.…(12分)
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $7+\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $\sqrt{46}+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
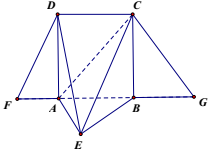 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com