
分析 设两个交点的坐标分别为(x1,y1),(x2,y2),利用点差法求得直线的斜率,进一步求出直线方程,然后验证直线与曲线方程由两个交点即可.
解答 解:设两个交点的坐标分别为(x1,y1),(x2,y2)
所以x12-4y12=4,x22-4y12=4,两式相减得(x1+x2)(x1-x2)=4(y1+y2)(y1-y2),
又$\frac{{x}_{1}+{x}_{2}}{2}$=3,$\frac{{y}_{1}+{y}_{2}}{2}$=-1,∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{4}$,
所以直线的方程为y+1=-$\frac{3}{4}$(x-3),即3x+4y-5=0.
由点A(3,-1)在双曲线内部,直线方程满足题意.
∴MN所在直线的方程是3x+4y-5=0.
故答案为:3x+4y-5=0.
点评 本题主要考查了直线与圆锥曲线的综合问题.解题的关键是充分运用数形结合的数学思想、方程的数学思想和转化的数学思想来解决较为复杂的综合题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+1,x∈[-2,2) | B. | f(x)=|3x-1|-|3x+1| | ||
| C. | f(x)=-x2+1,x∈(-2,+∞) | D. | f(x)=x4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
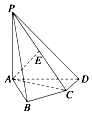 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉[1,2],x2-4x+6≥0 | B. | ?x0∈[1,2],x02-4x0+6≥0 | ||
| C. | ?x∉[1,2],x2-4x+6>0 | D. | ?x∈[1,2],x2-4x+6≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com