
| y2 |
| a2 |
| x2 |
| b2 |
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
| (1+22)[(x3+x4)2-4x3x4] |
| y2 |
| a2 |
| x2 |
| b2 |
| y2 |
| 4 |
| x2 |
| 3 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
|
| 3 |
| 4 |
| 9 |
| 16 |
| (1+22)[(x3+x4)2-4x3x4] |
5×[(-
|
| 15 |
| 4 |
| |0-2+1| | ||
|
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| ||
| 5 |
3
| ||
| 8 |


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
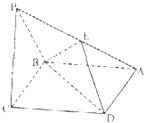 己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.
己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) | ||||
| 频数 | 40 | 70 | 79 | 162 | 59 | 55 | 35 | ||||
| 甲 厂 | 乙 厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
| P(Χ2≥k) | 0.100 0.050 0.025 0.010 0.001 |
| k | 2.706 3.841 5.024 6.635 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com