
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,E是AB的中点,F是BC的中点
(1)求证:EF∥平面A1DC1;
(2)若长方体ABCD﹣A1B1C1D1中,夹在平面A1DC1与平面B1EF之间的几何体的体积为![]() ,求点D到平面B1EF的距离.
,求点D到平面B1EF的距离.

【答案】(1)证明见详解;(2)2![]() .
.
【解析】
(1)因为![]() //
//![]() ,由线线平行,即可推证线面平行;
,由线线平行,即可推证线面平行;
(2)先根据几何体的体积求解出长方体的高,再用等体积法求得点到面的距离即可.
(1)证明:由题意,连接AC,如下图所示:
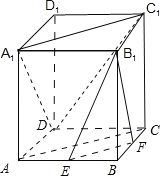
∵E是AB的中点,F是BC的中点,
∴EF∥AC,
∵四边形ACC1A1是平行四边形,
∴AC∥A1C1,
∴EF∥A1C1,
∵A1C1平面A1DC1,
∴EF∥平面A1DC1,即证.
(2)由题意,设长方体的高为h.
∵![]()
![]() 2
2![]() 2=2,
2=2,
∴![]()
![]()
![]()
![]() h
h![]() h.
h.
∵S△BEF![]()
![]() 1
1![]() 1
1![]() ,
,
∴![]()
![]() S△BEF
S△BEF![]() h
h![]()
![]()
![]()
![]() h
h![]() h.
h.
∵![]() 2
2![]() 2
2![]() h=4h,
h=4h,
∴4h![]() h
h![]() h
h![]() h
h![]() ,
,
解得h=2![]() .
.
又∵EF![]() ,DE=DF
,DE=DF![]() ,
,
容易知S△DEF![]() .
.
∴![]()
![]() S△DEF
S△DEF![]() B1B
B1B![]()
![]()
![]()
![]() 2
2![]() .
.
∵EF![]() ,B1E=B1F
,B1E=B1F![]() ,
,
∴![]() S△DEF
S△DEF![]() .
.
设点D到平面B1EF的距离为d.
∵![]() ,
,
∴![]()
![]()
![]()
![]() d
d![]() ,
,
解得d=2![]() .
.
∴点D到平面B1EF的距离为2![]() .
.


科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:

设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() 且右焦点
且右焦点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() .
.
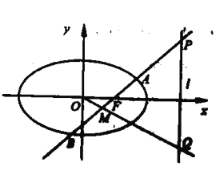
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() 是弦
是弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 与
与![]() 的面积之比是
的面积之比是![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosA=acosC+ccosA.
(1)求角A的大小;
(2)若a=3,△ABC的周长为8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2018,关于x的方程f(x)=2ax有唯一解,求a的值;
(3)当k=2019时,证明:对一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的两截面面积都相等,则两几何体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足祖暅原理,则该不规则几何体的体积为( )
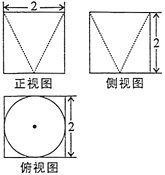
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com