【题目】记关于x的不等式 
的解集为P，不等式|x+2|＜3的解集为Q
（1）若a=3，求P；
（2）若P∪Q=Q，求正数a的取值范围．
【答案】
（1）解：a=3时， 
即 
，化简得 
∴集合 
，根据分式不等式的解法，解得﹣1＜x＜3
由此可得，集合P=（﹣1，3）
（2）解：Q={x||x+2|＜3}={x|﹣3＜x+2＜3}={x|﹣5＜x＜1}
可得Q=（﹣5，1）
∵a＞0，∴P={ 
}=（﹣1，a），
又∵P∪Q=Q，得PQ，
∴（﹣1，a）（﹣5，1），由此可得0＜a≤1
即正数a的取值范围是（0，1]
【解析】（1）当a=3时，分式不等式可化为 ，结合分式不等式解法的结论，即可得到解集P；（2）由含有绝对值不等式的解法，得Q=（﹣5，1）．根据a是正数，得集合P═（﹣1，a），并且集合P是Q的子集，由此建立不等式关系，即可得到正数a的取值范围．
同步练习强化拓展系列答案科目：高中数学 来源： 题型：
【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量
,求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，若A，B，C成等差数列，2a，2b，2c成等比数列，则cosAcosB=（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2015男篮亚锦赛决赛阶段，中国男篮以
连胜的不败成绩赢得第
届亚锦赛冠军，同时拿到亚洲唯一
张直通里约奥运会的入场券.赛后，中国男篮主力易建联荣膺本届亚锦赛
（最有价值球员），下表是易建联在这
场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
注：（1）表中
表示出手
次命中
次；
（2）
（真实得分率）是衡量球员进攻的效率，其计算公式为：
（1）从上述
场比赛中随机选择一场，求易建联在该场比赛中
超过
的概率；
（2）我们把比分分差不超过
分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况，从“胶着比赛”中随机选择两场，求易建联在这两场比赛中
至少有一场超过
的概率；
（3）用
来表示易建联某场的得分，用
来表示中国队该场的总分，画出散点图如图所示，请根据散点图判断
与
之间是否具有线性相关关系？结合实际简单说明理由.
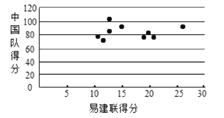
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设点
的坐标分别为
，直线
相交于点
，且它们的斜率之积是
.
（1）求点
的轨迹
的方程；
（2）直线
与曲线
相交于
两点，若
是否存在实数
，使得
的面积为
?若存在，请求出
的值；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数y=sinx的图象上所有的点向右平行移动 
个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是（ ）
A.y=sin（2x﹣ ）
B.y=sin（2x+ ）
C.y=sin（ 
x﹣ ）
D.y=sin（ x﹣ ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（2，﹣3）， 
=（﹣5，4）， 
=（1﹣λ，3λ+2）．
（1）若△ABC为直角三角形，且∠B为直角，求实数λ的值；
（2）若点A、B、C能构成三角形，求实数λ应满足的条件．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
+ 
，则下列命题中正确命题的序号是 ．
①f（x）是偶函数；
②f（x）的值域是[ 
，2]；
③当x∈[0， 
]时，f（x）单调递增；
④当且仅当x=2kπ± （k∈Z）时，f（x）= ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
