已知二次函数f(x)的二次项系数为a，且不等式f(x)>－2x的解集为(1,3)．
(1)若方程f(x)＋6a＝0有两个相等的根，求f(x)的解析式；
(2)若f(x)的最大值为正数，求实数a的取值范围．
(1)∵f(x)＋2x>0的解集为(1,3)，
∴f(x)＋2x＝a(x－1)(x－3)，且a<0，
即f(x)＝a(x－1)(x－3)－2x＝ax2－(2＋4a)x＋3a.①
由f(x)＋6a＝0，得
ax2－(2＋4a)＋9a＝0.②
∵方程②有两个相等的根，
∴Δ＝[－(2＋4a)]2－4a·9a＝0，
即5a2－4a－1＝0，解得a＝1或a＝－
.
由于a<0，故舍去a＝1，将a＝－代入①，
得f(x)＝－x2－
x－
.
(2)f(x)＝ax2－2(1＋2a)x＋3a
＝
由a<0，可得f(x)的最大值为－
>0，
由
解得a<－2－
或－2＋<a<0.
故当f(x)的最大值为正数时，实数a的取值范围是(－∞，－2－)∪(－2＋，0)．
科目：高中数学 来源： 题型：
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x＋T)＝Tf(x)成立．
(1)函数f(x)＝x是否属于集合M？说明理由；
(2)设f(x)∈M，且T＝2，已知当1<x<2时，f(x)＝x＋lnx，当－3<x<－2时，求f(x)的解析式．
查看答案和解析>>
科目：高中数学 来源： 题型：
设函数f(x)＝ax＋bx－cx，其中c>a>0，c>b>0.
(1)记集合M＝{(a，b，c)|a，b，c不能构成一个三角形的三条边长，且a＝b}，则(a，b，c)∈M所对应的f(x)的零点的取值集合为________；
(2)若a，b，c是△ABC的三条边长，则下列结论正确的是________．(写出所有正确结论的序号)
①∀x∈(－∞，1)，f(x)>0；
②∃x∈R，使ax，bx，cx不能构成一个三角形的三条边长；
③若△ABC为钝角三角形，则∃x∈(1,2)，使f(x)＝0.
查看答案和解析>>
科目：高中数学 来源： 题型：
设y1＝40.9，y2＝80.48，y3＝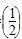
－1.5，则( )
A．y3>y1>y2 B．y2>y1>y3
C．y1>y2>y3 D．y1>y3>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则f(－1)＝( )
，2)在幂函数y＝f(x)的图像上，点(－
)在幂函数y＝g(x)的图像上，若f(x)＝g(x)，则x＝______.
则f(log43)＝________.