设二次函数f(x)=ax2+bx+c(a,b,c∈R),已知不论α,β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0.
(Ⅰ)求f(1)的值;
(Ⅱ)求证:c≥3a;
(Ⅲ)若a>0,函数f(sinα)的最大值为8,求b的值.
(本小题满分16分)
解:(1)取

,得f(sinα)=f(1)=a+b+c≥0
取β=π,得f(2+cosβ)=f(1)=a+b+c≤0
∴f(1)=0
(2)证:取β=0,得f(2+cosβ)=f(3)=9a+3b+c≤0
由(1)得f(1)=a+b+c=0,∴b=-(a+c)代入得9a-3(a+c)+c≤0
∴c≥3a
(3)设sinx=t,则-1≤t≤1又b=-(a+c),
∴f(sinx)=f(t)=at
2-(a+c)t+c=a
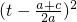
+c-
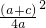
,
∵a>0,c≥3a,
∴
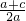
≥
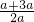
=2,
∴二次函数f(t)在t∈[-1,1]上递减
∴t=-1时,f(x)
最大=a+(a+c)+c=8
∴a+c=4,b=-(a+c)=-4.
分析:(1)取α=

,β=π,可求得f(1)=a+b+c≥0,f(1)=a+b+c≤0,从而f(1)=0;
(2)取β=0,有f(3)=9a+3b+c≤0,而f(1)=a+b+c=0,可得b=-(a+c),代入9a-3(a+c)+c≤0可得c≥3a;
(3)设sinx=t,f(sinx)=f(t)=a
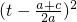
+c-
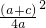
,由a>0,c≥3a,可求得
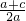
≥2,从而可得二次函数f(t)在t∈[-1,1]上递减,而f(x)
最大=8,问题解决.
点评:本题考查二次函数在闭区间上的最值,着重考查恒成立问题与二次函数的性质的应用,换元后分析出其对称轴t=
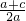
≥2是关键,属于难题.

 ,得f(sinα)=f(1)=a+b+c≥0
,得f(sinα)=f(1)=a+b+c≥0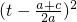 +c-
+c-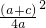 ,
,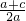 ≥
≥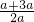 =2,
=2, ,β=π,可求得f(1)=a+b+c≥0,f(1)=a+b+c≤0,从而f(1)=0;
,β=π,可求得f(1)=a+b+c≥0,f(1)=a+b+c≤0,从而f(1)=0;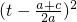 +c-
+c-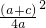 ,由a>0,c≥3a,可求得
,由a>0,c≥3a,可求得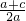 ≥2,从而可得二次函数f(t)在t∈[-1,1]上递减,而f(x)最大=8,问题解决.
≥2,从而可得二次函数f(t)在t∈[-1,1]上递减,而f(x)最大=8,问题解决.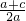 ≥2是关键,属于难题.
≥2是关键,属于难题. 
