
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AB=BC=![]() ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
(1)AF为何值时,CF⊥平面B1DF?
(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.

(1)AF=1或2时,CF⊥平面B1DF
(2)锐二面角的余弦值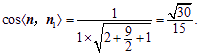
(1)因为直三棱柱ABC-A1B1C1中,
BB1⊥面ABC,∠ABC=![]() .
.
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
因为AC=2,∠ABC=90??,所以AB=BC=,
从而B(0,0,0),A![]() ,C
,C![]() ,B1(0,0,3),A1
,B1(0,0,3),A1![]() ,C1
,C1![]() ,D
,D![]() ,E
,E![]() .
.
 所以
所以![]() ,
,
设AF=x,则F(,0,x),
![]() .
.
![]() ,所以
,所以![]()
要使CF⊥平面B1DF,只需CF⊥B1F.
由![]() =2+x(x-3)=0,得x=1或x=2,
=2+x(x-3)=0,得x=1或x=2,
故当AF=1或2时,CF⊥平面B1DF.……………… 5分
(2)由(1)知平面ABC的法向量为n1=(0,0,1).
设平面B1CF的法向量为![]() ,则由
,则由![]() 得
得![]()
令z=1得![]() ,
,
所以平面B1CF与平面ABC所成的锐二面角的余弦值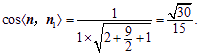
………………… 10分


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.| AF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com