Question

14．已知一个算法的程序框图如图所示，当输出的结果为0时，输入的x的值为（　　）

• A． -2
• B． -2或-1
• C． 1或-3
• D． -2或$\frac{1}{3}$

Answer 1

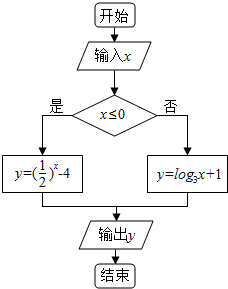
分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出分段函数y=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}-4}&{x≤0}\\{lo{g}_{3}^{x}+1}&{x＞0}\end{array}\right.$的函数值．

解答 解：分析程序中各变量、各语句的作用，
再根据流程图所示的顺序，可知：
该程序的作用是计算并输出分段函数y=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}-4}&{x≤0}\\{lo{g}_{3}^{x}+1}&{x＞0}\end{array}\right.$的函数值．
当x≤0时，由y=（$\frac{1}{2}$）^x-4=0，可得：x=-2；
当x＞0时，由y=log${\;}_{3}^{x}$+1=0，可得：x=$\frac{1}{3}$；
故选：D．

点评 算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．