
(30分)如图,已知抛物线C:![]() ,F为C的焦点,l为准线,且l交x轴于E点,过点F任意作一条直线交抛物线C于A、B两点。
,F为C的焦点,l为准线,且l交x轴于E点,过点F任意作一条直线交抛物线C于A、B两点。
(1)若![]() ,求证:
,求证:![]() ;
;
(2)设M为线段AB的中点,P为奇素数,且点M到x轴的距离和点M到准线l的距离均为非零整数,求证:点M到坐标原点O的距离不可能是整数。

解析:(1)方法1:点F的坐标为(p,0),设直线l的方程为![]()
得![]() ①
①
设![]() ,则y1、y2是方程①的两个根,有
,则y1、y2是方程①的两个根,有
![]()
由![]()
因为![]() ,
,
又![]()
所以![]()
![]()
故![]() …………10分
…………10分
方法2:如图,设点A、B在准线l上的射影分别为A′、B′,
则|AF|=|A′A|,|BF|=|B′B|。从而,由![]()
因为![]()
又![]()
故![]() …………10分
…………10分
(2)设M(x,y),依题意x、y均为非零整数,由对称性,不防设x,y![]() ,则
,则
![]() ②
②
因为点M在直线AB上,所以x=my+p ③
由②、③消去m,得![]() ④
④
假设|OM|=r为正整数,则 ![]() ⑤
⑤
因为p为奇质数,所以由④知,p|y,从而p|x。
于是,由⑤知p|r。
令![]() ,则有
,则有
![]() 。
。
消去y1,得![]()
即![]()
又![]() 有相同的奇偶性,且
有相同的奇偶性,且![]()
所以
从而y1=0,于是y=-0,这与y为正整数矛盾。
故点M到坐标顶点O的距离不可能是整数。



科目:高中数学 来源: 题型:
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且
如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.| TA |
| TB |
查看答案和解析>>
科目:高中数学 来源: 题型:
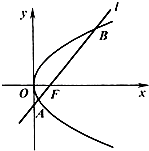 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com