已知圆C过原点O,且与直线x+y=4相切于点A(2,2).
(1)求圆C的方程;
(2)过原点O作射线交圆C于另一点M,交直线x=3于点N.
①OM•ON是否存在最小值?若存在,求出最小值;若不存在,请说明理由;
②若射线OM上一点P(x,y)满足OP2=OM•ON,求证:x3+xy2-6x-6y=0.
【答案】
分析:(1)根据题意得到圆心即为线段OA的中点,求出线段OA中点坐标即为圆心,求出圆心到A的距离即为半径r,写出圆C方程即可;
(2)①设射线方程为y=kx,代入圆C方程,消去y得到关于x的一元二次方程,求出M的横坐标,根据射线与x=3相交,得到M横坐标与3同号,确定出k大于-1,利用两点的距离公式表示出OM•ON,化简后根据k的范围确定出其值不存在最小值;
②由P坐标表示出OP,将OM•ON与OP的值代入OP
2=OM•ON,再将k=

代入化简即可得证.
解答:解:(1)由题意得:圆心为OA的中点(1,1),半径r=
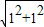
=
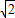
,
∴圆C的方程为(x-1)
2+(y-1)
2=2;
(2)①设射线所在直线方程为y=kx,
将它代入(x-1)
2+(y-1)
2=2得:(k
2+1)x
2-(2k+2)x=0,
∴x
M=
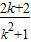
,
∵射线y=kx与直线x=3相交,
∴x
M与3同号,
∴k>-1,
∴OM•ON=
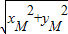
•
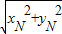
=

•
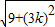
=3|2k+2|=6k+6,
∵k>-1,
∴OM•ON无最小值;
②证明:∵OP
2=OM•ON,
∴x
2+y
2=6k+6,
又y
=kx
,
∴k=

代入上式得:x
3+x
y
2-6x
-6y
=0.
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两点间的距离公式,线段中点坐标公式,直线斜率,熟练掌握公式是解本题的关键.

 代入化简即可得证.
代入化简即可得证.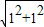 =
=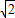 ,
,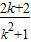 ,
,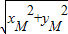 •
•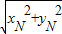 =
= •
•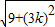 =3|2k+2|=6k+6,
=3|2k+2|=6k+6, 代入上式得:x3+xy2-6x-6y=0.
代入上式得:x3+xy2-6x-6y=0.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案