
(本小题满分14分)已知函数
(1)当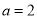 时,求函数
时,求函数 的最值;
的最值;
(2)当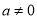 时,过原点分别作曲线
时,过原点分别作曲线 和
和 的切线
的切线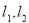 ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明:
(1)最大值为 无最小值 (2)详见解析
无最小值 (2)详见解析
【解析】
试题分析:第(1)问利用导数求函数的单调区间,求解函数的最值;第(2)问背景为指数函数 与对数函数
与对数函数 关于直线
关于直线 对称的特征,得到过原点的切线也关于直线
对称的特征,得到过原点的切线也关于直线 对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明.
对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明.
试题解析:(1)当 时,
时, ,定义域为
,定义域为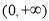 .
.
对 求导,得
求导,得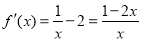 .
.
当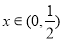 时,
时,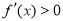 ,当
,当 时,
时, ,即函数
,即函数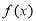 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以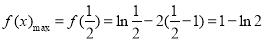 ,没有最小值.
,没有最小值.
(2)设切线 的方程为
的方程为 ,切点为
,切点为 ,则
,则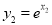 ,
,
 ,所以
,所以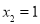 ,
, ,则
,则 .
.
由题意知,切线 的斜率为
的斜率为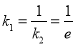 ,
, 的方程为
的方程为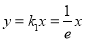 .
.
设 与曲线
与曲线 的切点为
的切点为 ,则
,则 ,
,
所以 ,
,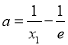 .
.
又因为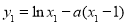 ,消去
,消去 和
和 后,整理得
后,整理得 .
.
令 ,则
,则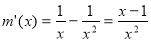 ,
, 在
在 上单调递减,在
上单调递减,在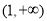 上单调递增.
上单调递增.
若 ,因为
,因为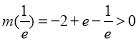 ,
,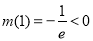 ,所以
,所以 ,
,
而 在
在 上单调递减,所以
上单调递减,所以 .
.
若 ,因为
,因为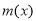 在
在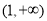 上单调递增,且
上单调递增,且 ,则
,则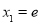 ,
,
所以 (舍去).
(舍去).
综上可知, .
.
考点:导数的几何意义,函数的单调性、最值.


科目:高中数学 来源:2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考文科数学试卷(解析版) 题型:选择题
已知定义在R上的偶函数f(x)满足f(4-x)=f(x),且当x∈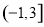 时,
时, 则g(x)= f(x)-|1gx|的零点个数是( )
则g(x)= f(x)-|1gx|的零点个数是( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考理科数学试卷(解析版) 题型:选择题
已知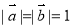 向量
向量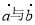 的夹角为120°,且
的夹角为120°,且 ,则实数t的值为( )
,则实数t的值为( )
 .-1 B.1 C.-2 D.2
.-1 B.1 C.-2 D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品文科数学试卷(解析版) 题型:填空题
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理“幂势既同,则积不容异.”
这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.设由曲线 和直线
和直线 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为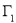 ;由同时满足
;由同时满足 的点
的点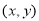 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为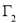 ;根据祖暅原理等知识,通过考察
;根据祖暅原理等知识,通过考察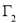 可以得到
可以得到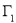 的体积为 .
的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品文科数学试卷(解析版) 题型:选择题
已知双曲线 :
: 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于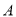 ,
, 两点,
两点,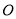 为坐标原点,若双曲线
为坐标原点,若双曲线 的离心率为2,
的离心率为2, 的面积为
的面积为 ,则
,则 的内切圆半径为( )
的内切圆半径为( )
A. B.
B. C.
C.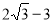 D.
D.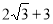
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:填空题
(1)若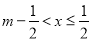 (其中
(其中 为正数),则称
为正数),则称 为离实数
为离实数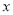 最近的正数,记作
最近的正数,记作 ,即
,即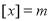
 ,则
,则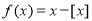 的值域是 ;
的值域是 ;
(2)设集合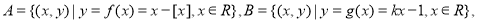 若集合
若集合 的子集恰有4个,则实数
的子集恰有4个,则实数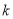 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测理科数学试卷(解析版) 题型:解答题
如图:三棱锥P-ABC中,PA底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为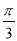 .若
.若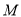 是
是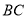 的中点,求:
的中点,求:
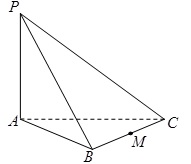
(1)三棱锥P-ABC的体积;
(2)异面直线PM与AC所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com