
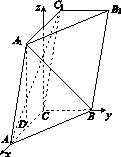
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
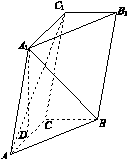
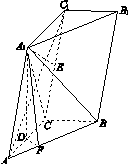
解:方法一:(1)证明:因为A1D⊥平面ABC,A1D⊂平面AA1C1C,故平面AA1C1C⊥平面ABC.
又BC⊥AC,所以BC⊥平面AA1C1C.
连接A1C,因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1,故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
又直线AA1∥平面BCC1B1,因而A1E为直线AA1与平面BCC1B1的距离,
即A1E= .
.
因为A1C为∠ACC1的平分线,
所以A1D=A1E= .
.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,故∠A1FD为二面角A1 AB C的平面角.
由AD=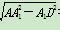 =1,得D为AC中点,
=1,得D为AC中点,
DF=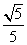 ,tan∠A1FD=
,tan∠A1FD=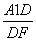 =
=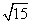 ,所以cos∠A1FD=
,所以cos∠A1FD=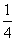 .
.
所以二面角A1 AB C的大小为arccos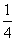 .
.
方法二:以C为坐标原点,射线CA为x轴的正半轴,以CB的长为单位长,建立如图所示的空间直角坐标系C xyz.由题设知A1D与z轴平行,z轴在平面AA1C1C内.

 -p+
-p+ r=0,且-2p+q=0.
r=0,且-2p+q=0.
令p= ,则q=2
,则q=2  ,r=1,所以n=(
,r=1,所以n=( ,2
,2  ,1).
,1).
又p=(0,0,1)为平面ABC的法向量,故
cos〈n,p〉=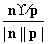 =
=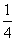 .
.
所以二面角A1 AB C的大小为arccos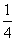 .
.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
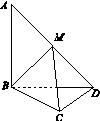
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)
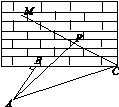
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知棱长为1的正方体ABCD A1B1C1D1中,P,Q是面对角线A1C1上的两个不同的动点.
给出以下四个结论:
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若PQ=1,则四面体BDPQ的体积一定是定值;
④若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上各结论中,正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(1)若从袋中一次摸出2个小球,求恰为异色球的概率;
(2)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为ξ,求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com