
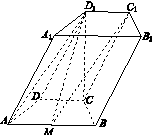
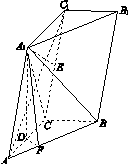
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
解:(1)证明:因为四边形ABCD是等腰梯形,
且AB=2CD,所以AB∥DC,
又M是AB的中点,
所以CD∥MA且CD=MA.
连接AD1.因为在四棱柱ABCD A1B1C1D1中,
CD∥C1D1,CD=C1D1,
所以C1D1∥MA,C1D1=MA,
所以四边形AMC1D1为平行四边形,
因此,C1M∥D1A.
又C1M⊄平面A1ADD1,D1A⊂平面A1ADD1,
所以C1M∥平面A1ADD1.
(2)方法一:连接AC,MC.
由(1)知,CD∥AM且CD=AM,
所以四边形AMCD为平行四边形,
所以BC=AD=MC.
由题意∠ABC=∠DAB=60°,
所以△MBC为正三角形,
因此AB=2BC=2,CA= ,
,
因此CA⊥CB.
设C为坐标原点,建立如图所示的空间直角坐标系C xyz.

所以A( ,0,0),B(0,1,0),D1(0,0,
,0,0),B(0,1,0),D1(0,0, ).
).
因此M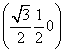 ,
,
所以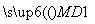 =
=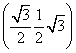 ,
,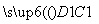 =
=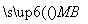 =
=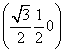 .
.
设平面C1D1M的一个法向量n=(x,y,z),
由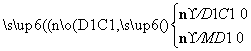 得
得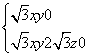
可得平面C1D1M的一个法向量n=(1, ,1).
,1).
又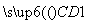 =(0,0,
=(0,0, )为平面ABCD的一个法向量.
)为平面ABCD的一个法向量.
因此cos〈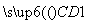 ,n〉=
,n〉=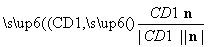 =
=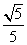 ,
,
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为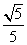 .
.
方法二:由(1)知,平面D1C1M∩平面ABCD=AB,点过C向AB引垂线交AB于点N,连接D1N.
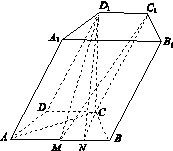
由CD1⊥平面ABCD,可得D1N⊥AB,
因此∠D1NC为二面角C1 AB C的平面角.
在Rt△BNC中,BC=1,∠NBC=60°,
可得CN= ,
,
所以ND1=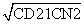 =
=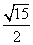 .
.
在Rt△D1CN中,cos∠D1NC=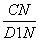 =
=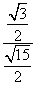 =
=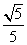 ,
,
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为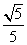 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球.否则一直发到3次为止,设学生一次发球成功的概率为p(p≠0),发球次数为X, 若X的数学期望E(X)>1.75,则p的取值范围是( )

查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
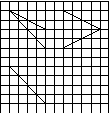
图13
A.6  B.6 C.4
B.6 C.4  D.4
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
A.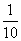 B.
B.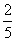 C.
C.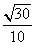 D.
D.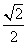
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
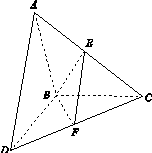
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
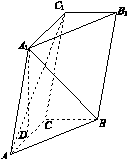
查看答案和解析>>
科目:高中数学 来源: 题型:
根据世行2013年新标准,人均GDP低于1 035美元为低收入国家;人均GDP为1 035~4 085美元为中等偏下收入国家;人均GDP为4 085~12 616美元为中等偏上收入国家;人均GDP不低于12 616美元为高收入国家.某城市有5个行政区,各区人口占该城市人口比例及人均GDP如下表:
| 行政区 | 区人口占城市人口比例 | 区人均GDP(单位:美元) |
| A | 25% | 8 000 |
| B | 30% | 4 000 |
| C | 15% | 6 000 |
| D | 10% | 3 000 |
| E | 20% | 10 000 |
(1)判断该城市人均GDP是否达到中等偏上收入国家标准;
(2)现从该城市5个行政区中随机抽取2个,求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com