
三棱锥P ABC中,D,E分别为PB,PC的中点,记三棱锥D ABE的体积为V1,P ABC的体积为V2,则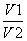 =________.
=________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在如图11所示的空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )
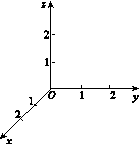
图11
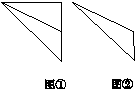
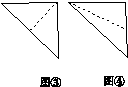
A.①和② B.①和③ C.③和② D.④和②
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
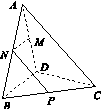
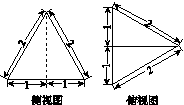
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
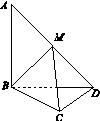
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
已知棱长为1的正方体ABCD A1B1C1D1中,P,Q是面对角线A1C1上的两个不同的动点.
给出以下四个结论:
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若PQ=1,则四面体BDPQ的体积一定是定值;
④若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上各结论中,正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
.一位客人游览福州鼓山、福州永泰天门山、福州青云山这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设Y表示客人离开福州市时游览的景点数与没有游览的景点数之差的绝对值.求Y的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com