练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    体育课的排球发球项目考试的规则是：每位学生最多可发球3次，一旦发球成功，则停止发球．否则一直发到3次为止，设学生一次发球成功的概率为p(p≠0)，发球次数为X, 若X的数学期望E(X)>1.75，则p的取值范围是(　　)


    　C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    用0,1,2,3,4,5,6构成无重复数字的七位数，其中：

    (1)能被25整除的数有多少个？

    (2)设x，y，z分别表示个位、十位、百位上的数字，满足x<y<z的数有多少个？

    (3)偶数必须相邻的数有多少个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在区间[－3,3]上随机取一个数x，使得|x＋1|－|x－2|≥1成立的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B为两个事件，若事件A和B同时发生的概率为，在事件A发生的条件下，事件B发生的概率为，事件A发生的概率为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知某一随机变量X的概率分布列如下，且E(X)＝6.3，则a的值为(　　)

    X

    4

    a

    9

    P

    0.5

    0.1

    b

    A.5                                     B．6

    C．7                                    D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为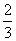，乙获胜的概率为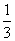，各局比赛结果相互独立．

    (1)求甲在4局以内(含4局)赢得比赛的概率；

    (2)记X为比赛决出胜负时的总局数，求X的分布列和均值(数学期望)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在如图1­1所示的空间直角坐标系O ­ xyz中，一个四面体的顶点坐标分别是(0，0，2)，(2，2，0)，(1，2，1)，(2，2，2)．给出编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为(　　)

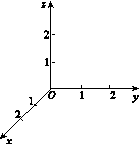
    图1­1

     　

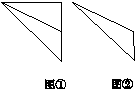
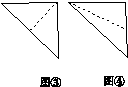
    A．①和②  B．①和③  C．③和②  D．④和②

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­3所示，在四棱柱ABCD ­A1B1C1D1中，底面ABCD是等腰梯形，∠DAB＝60°，AB＝2CD＝2，M是线段AB的中点．

    图1­3

    (1)求证：C1M∥平面A1ADD1；

    (2)若CD1垂直于平面ABCD且CD1＝，求平面C1D1M和平面ABCD所成的角(锐角)的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知棱长为1的正方体ABCD ­A1B1C1D1中，P，Q是面对角线A1C1上的两个不同的动点．

    给出以下四个结论：

    ①存在P，Q两点，使BP⊥DQ；

    ②存在P，Q两点，使BP，DQ与直线B1C都成45°的角；

    ③若PQ＝1，则四面体BDPQ的体积一定是定值；

    ④若PQ＝1，则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值．

    以上各结论中，正确结论的个数是(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    同步练习册答案