
甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为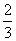 ,乙获胜的概率为
,乙获胜的概率为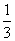 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
解 用A表示“甲在4局以内(含4局)赢得比赛”,Ak表示“第k局甲获胜”,Bk表示“第k局乙获胜”,则P(Ak)=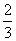 ,P(Bk)=
,P(Bk)=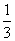 ,k=1,2,3,4,5.
,k=1,2,3,4,5.
(1)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)
=P(A1)P(A2)+P(B1)P(A2)P(A3)+P(A1)P(B2)·P(A3)P(A4)
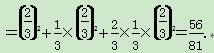 (2)X的可能取值为2,3,4,5.
(2)X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)=P(A1)P(A2)+P(B1)P(B2)=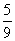 ,
,
P(X=3)=P(B1A2A3)+P(A1B2B3)
=P(B1)P(A2)P(A3)+P(A1)P(B2)P(B3)= ,
,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)
=P(A1)P(B2)P(A3)P(A4)
+P(B1)P(A2)P(B3)·P(B4)=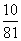 .
.
P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=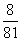 .
.
故X的分布列为
| X | 2 | 3 | 4 | 5 |
| P |
|
|
|
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分.某考生每道题都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道题能排除两个错误选项,另2道只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机选一个选项作答,且各题作答互不影响.
(1)求该考生本次测验选择题得50分的概率;
(2)求该考生本次测验选择题所得分数的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球.否则一直发到3次为止,设学生一次发球成功的概率为p(p≠0),发球次数为X, 若X的数学期望E(X)>1.75,则p的取值范围是( )

查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
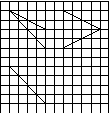
图13
A.6  B.6 C.4
B.6 C.4  D.4
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
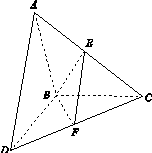
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图J124所示,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
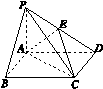
图J124
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com