
如图J124所示,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
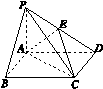
图J124
解:方法一:
(1)证明:∵PA⊥平面ABCD,CD⊂平面ABCD,
∴PA⊥CD.
又∵四边形ABCD是矩形,∴AD⊥CD.
又PA∩AD=A,PA,AD⊂平面PAD,∴CD⊥平面PAD.
又∵CD⊂平面PDC,∴平面PDC⊥平面PAD.
(2)取AD的中点O,连接EO,则EO∥PA.
∵PA⊥平面ABCD,∴EO⊥平面ABCD.
过点O作OF⊥AC交AC于点F,连接EF,
则∠EFO就是二面角EACD的平面角.
由PA=2,得EO=1.
在Rt△ADC中,由AD·CD=AC·h,得h=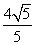 .
.
又∵O是AD的中点,OF⊥AC,∴OF=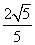 .
.
而EO=1,由勾股定理可得EF=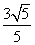 ,
,
故cos∠EFO=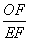 =
=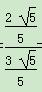 =
=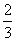 ,即二面角E AC D的余弦值为
,即二面角E AC D的余弦值为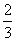 .
.

(3)延长AE,过点D作DG垂直AE于点G,连接CG.
由(1)可知,CD⊥AE,又CD∩DG=D,∴AE⊥平面CDG.
过点D作DH垂直CG于点H,则AE⊥DH.
又CG∩AE=G,∴DH⊥平面AGC,即DH⊥平面AEC,
∴CD在平面ACE内的射影是CH,
∴∠DCH是直线CD与平面AEC所成的角.
∵DG=AD·sin∠DAG=AD·sin∠OAE=AD·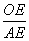 =
=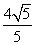 ,
,
又在Rt△CDG中,CD=2,∴CG=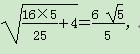
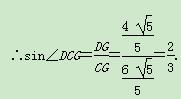
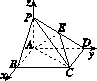
方法二:如图,以为A原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),E(0,2,1),P(0,0,2),
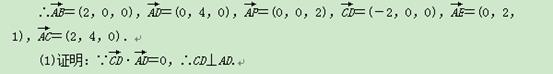
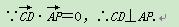
又∵AP∩AD=A,∴CD⊥平面PAD.
又∵CD⊂平面PDC,∴平面PDC⊥平面PAD.
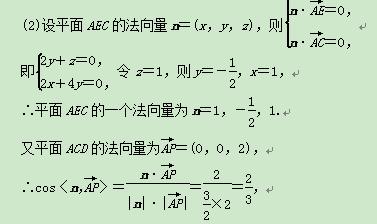 ∴二面角EACD的余弦值是
∴二面角EACD的余弦值是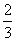 .
.
(3)设直线CD与平面AEC所成的角为θ.
∵平面AEC的一个法向量为n=1,- ,1,
,1,
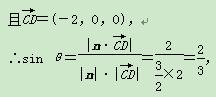 即直线CD与平面AEC所成角的正弦值为
即直线CD与平面AEC所成角的正弦值为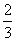 .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为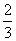 ,乙获胜的概率为
,乙获胜的概率为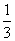 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)
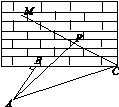
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知棱长为1的正方体ABCD A1B1C1D1中,P,Q是面对角线A1C1上的两个不同的动点.
给出以下四个结论:
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若PQ=1,则四面体BDPQ的体积一定是定值;
④若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上各结论中,正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(1)若从袋中一次摸出2个小球,求恰为异色球的概率;
(2)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线方程3x+2y﹣6=0的斜率为k,在y轴上的截距为b,则有( )
A. k=﹣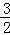 ,b=3 B. k=﹣
,b=3 B. k=﹣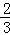 ,b=﹣3 C. k=﹣
,b=﹣3 C. k=﹣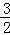 ,b=﹣3 D. k=﹣
,b=﹣3 D. k=﹣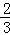 ,b=3
,b=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com