
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(1)若从袋中一次摸出2个小球,求恰为异色球的概率;
(2)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为ξ,求ξ的分布列.
科目:高中数学 来源: 题型:
如图13,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
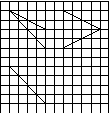
图13
A.6  B.6 C.4
B.6 C.4  D.4
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
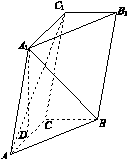
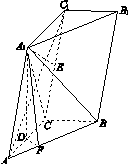
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图J124所示,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
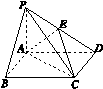
图J124
查看答案和解析>>
科目:高中数学 来源: 题型:
某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是( )
A.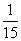 B.
B.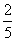
C.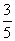 D.
D.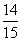
查看答案和解析>>
科目:高中数学 来源: 题型:
根据世行2013年新标准,人均GDP低于1 035美元为低收入国家;人均GDP为1 035~4 085美元为中等偏下收入国家;人均GDP为4 085~12 616美元为中等偏上收入国家;人均GDP不低于12 616美元为高收入国家.某城市有5个行政区,各区人口占该城市人口比例及人均GDP如下表:
| 行政区 | 区人口占城市人口比例 | 区人均GDP(单位:美元) |
| A | 25% | 8 000 |
| B | 30% | 4 000 |
| C | 15% | 6 000 |
| D | 10% | 3 000 |
| E | 20% | 10 000 |
(1)判断该城市人均GDP是否达到中等偏上收入国家标准;
(2)现从该城市5个行政区中随机抽取2个,求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com