
如图14,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)
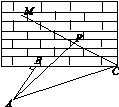
图14
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分.某考生每道题都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道题能排除两个错误选项,另2道只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机选一个选项作答,且各题作答互不影响.
(1)求该考生本次测验选择题得50分的概率;
(2)求该考生本次测验选择题所得分数的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
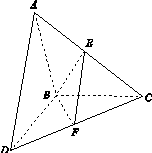
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
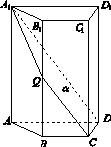
图15
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
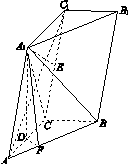
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
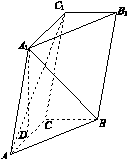
查看答案和解析>>
科目:高中数学 来源: 题型:
如图12,在正方体ABCD A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是( )

图12
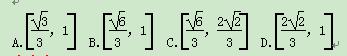
查看答案和解析>>
科目:高中数学 来源: 题型:
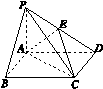
如图J124所示,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
图J124
查看答案和解析>>
科目:高中数学 来源: 题型:
某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是( )
A.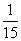 B.
B.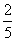
C.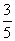 D.
D.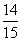
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=4和点M(1,a).
(1)若过点M有且只有一条直线与圆O相切,求正数a的值,并求出切线方程;
(2)若a=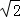 ,过点M的圆的两条弦AC,BD互相垂直.
,过点M的圆的两条弦AC,BD互相垂直.
①求四边形ABCD面积的最大值;②求|AC|+|BD|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com