
已知圆O:x2+y2=4和点M(1,a).
(1)若过点M有且只有一条直线与圆O相切,求正数a的值,并求出切线方程;
(2)若a=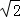 ,过点M的圆的两条弦AC,BD互相垂直.
,过点M的圆的两条弦AC,BD互相垂直.
①求四边形ABCD面积的最大值;②求|AC|+|BD|的最大值.
解:(1)由条件知点M在圆O上,所以1+a2=4,则a=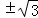 ,
,
由a>0,则a= ,点M为(1,
,点M为(1, ),kOM=
),kOM= ,切线的斜率为﹣
,切线的斜率为﹣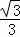 ,
,
此时切线方程为y﹣ =﹣
=﹣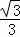 (x﹣1),即x+
(x﹣1),即x+ y﹣4=0;
y﹣4=0;
(2)设O到直线AC,BD的距离分别为d1,d2,
则d12+d22=|OM|2=3,于是|AC|=2 ,|BD|=2
,|BD|=2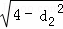 ,
,
①SABCD=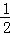 |AC|•|BD|=2
|AC|•|BD|=2 •
•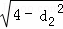 ≤4﹣d12+4﹣d22=8﹣3=5,
≤4﹣d12+4﹣d22=8﹣3=5,
当且仅当d1=d2=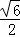 时取等号,
时取等号,
即四边形ABCD面积的最大值为5;
②|AC|+|BD|=2 +2
+2 ,
,
则(|AC|+|BD|)2=4(4﹣d12+4﹣d22+2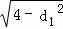 •
• )
)
=4(5+2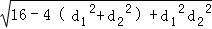 )=4(5+2
)=4(5+2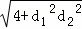 )
)
因为2d1d2≤d12+d22=3,所以d12d22≤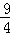 ,当且仅当d1=d2=
,当且仅当d1=d2=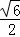 时取等号,
时取等号,
所以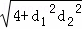 ≤
≤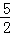 ,所以(|AC|+|BD|)2≤4(5+2×
,所以(|AC|+|BD|)2≤4(5+2×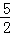 )=40,
)=40,
所以|AC|+|BD|≤2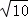 ,
,
即|AC|+|BD|的最大值为2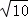 .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
如图14,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)
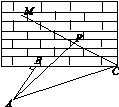
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
正三棱柱ABC﹣A1B1C1中,底面边长为2,若异面直线AB1与BC1所成的角为60°,则该三棱柱的侧棱长为( )
A. 2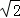 或
或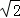 B.
B. 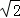 C.
C. 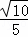 D. 2
D. 2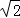
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量36样本,则老年人、中年人、青年人分别各抽取的人数是( )
A. 6,12,18 B. 7,11,19 C. 6,13,17 D. 7,12,17
查看答案和解析>>
科目:高中数学 来源: 题型:
直线方程3x+2y﹣6=0的斜率为k,在y轴上的截距为b,则有( )
A. k=﹣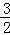 ,b=3 B. k=﹣
,b=3 B. k=﹣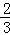 ,b=﹣3 C. k=﹣
,b=﹣3 C. k=﹣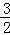 ,b=﹣3 D. k=﹣
,b=﹣3 D. k=﹣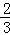 ,b=3
,b=3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:x2+2x﹣3>0;命题q:x>a,且¬q的一个充分不必要条件是¬p,则a的取值范围是( )
A.a≥1 B. a≤1 C. a≥﹣1 D. a≤﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
若f(x)=-x2+2ax与g(x)=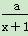 在区间[1,2]上都是减函数,则a的取值范围是( )
在区间[1,2]上都是减函数,则a的取值范围是( )
A.(-1,0)∪(0,1) B.(-1,0)∪(0,1]
C.(0,1) D.(0,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com