
如图12,在正方体ABCD A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是( )

图12
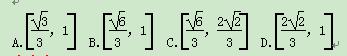
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
如图13所示,四棱锥PABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=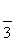 ,M为BC上一点,且BM=
,M为BC上一点,且BM= ,MP⊥AP.
,MP⊥AP.
(1)求PO的长;
(2)求二面角APMC的正弦值.
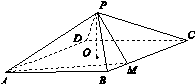
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
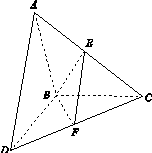
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)
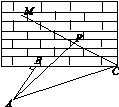
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
如图J112①所示,四边形ABCD为等腰梯形,AE⊥DC,AB=AE=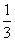 DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
(1)求证:平面PAF⊥平面PBE;
(2)求三棱锥APBC与三棱锥EBPF的体积之比.
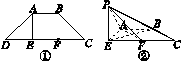
图J112
查看答案和解析>>
科目:高中数学 来源: 题型:
盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量36样本,则老年人、中年人、青年人分别各抽取的人数是( )
A. 6,12,18 B. 7,11,19 C. 6,13,17 D. 7,12,17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com