
如图J112①所示,四边形ABCD为等腰梯形,AE⊥DC,AB=AE=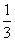 DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
(1)求证:平面PAF⊥平面PBE;
(2)求三棱锥APBC与三棱锥EBPF的体积之比.
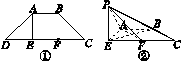
图J112
解:(1)证明:连接BF,∵EF∥AB,且AB=EF=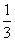 CD,
CD,
∴四边形AEFB为平行四边形.
又∵AE=AB,且AE⊥DC,
∴四边形AEFB为正方形,∴AF⊥BE.
∵平面PAE⊥平面ABCE,且平面PAE∩平面ABCE=AE,PE⊥AE,
∴PE⊥平面ABCE.又AF⊂平面ABCE,∴PE⊥AF.
又∵BE∩PE=E,∴AF⊥平面PBE.
又∵AF⊂平面PAF,∴平面PAF⊥平面PBE.
(2)不妨设AB=4,
则V三棱锥A PBC=V三棱锥P ABC=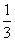 ×
× ×4×4×4=
×4×4×4=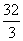 ,
,
V三棱锥E BPF=V三棱锥P EBF=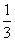 ×
× ×4×4×4=
×4×4×4=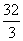 .
.
故所求两个三棱锥的体积之比为1∶1.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
某高校进行自主招生面试时的程序如下:共设3道题,每道题答对给10分,答错倒扣5分(每道题都必须回答,但相互不影响).设某学生对每道题答对的概率为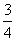 ,则该学生在面试时得分的期望为________.
,则该学生在面试时得分的期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
一块石材表示的几何体的三视图如图12所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
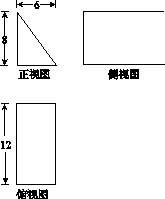
图12
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
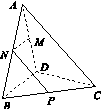
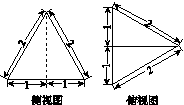
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
如图12,在正方体ABCD A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是( )

图12
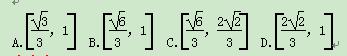
查看答案和解析>>
科目:高中数学 来源: 题型:
中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
|
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 |
| 男生 | 800 | 440 | 200 |
| 女生 | 200 | 160 | 200 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知“跟从别人闯红灯”的人中抽取50人,求n的值.
(2)在“带头闯红灯”的人中,将男生的200人编号为001,002,…,200;将女生的200人编号为201,202,…,400,用系统抽样的方法抽取5人参加“文明交通”宣传活动,若抽取的第一个人的编号为30,把抽取的5人看成一个总体,从这5人中任选取2人,求至少有一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com