练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     一块石材表示的几何体的三视图如图1­2所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于(　　)

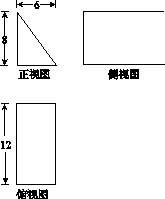
    图1­2

    A．1  B．2  C．3  D．4


    B　[解析] 由三视图可知，石材为一个三棱柱(相对应的长方体的一半)，故可知能得到的最大球为三棱柱的内切球．由题意可知正视图三角形的内切圆的半径即为球的半径，可得r＝＝2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示，在单位圆O的某一直径上随机的取一点Q，求过点Q且与该直径垂直的弦长长度不超过1的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体三视图如图1­1所示，则该几何体的体积为(　　)

    A．8－2π  B．8－π  C．8－  D．8－

    图1­1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图1­6所示，四棱柱ABCD ­A1B1C1D1的所有棱长都相等，AC∩BD＝O，A1C1∩B1D1＝O1，四边形ACC1A1和四边形BDD1B1均为矩形．

    (1)证明：O1O⊥底面ABCD；

    (2)若∠CBA＝60°，求二面角C1­OB1­D的余弦值．

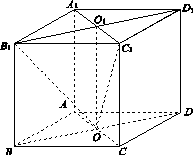
    图1­6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­3所示，四棱锥P­ABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB＝2，∠BAD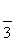＝，M为BC上一点，且BM＝，MP⊥AP.

    (1)求PO的长；

    (2)求二面角A­PM­C的正弦值．

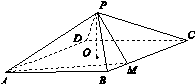
    图1­3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­3，四棱锥P­ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

    (1)证明：PB∥平面AEC；

    (2)设二面角D­AE­C为60°，AP＝1，AD＝，求三棱锥E­ACD的体积．

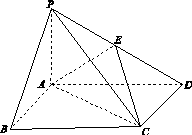
    图1­3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­5所示，△ABC和△BCD所在平面互相垂直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F分别为AC，DC的中点．

    (1)求证：EF⊥BC；

    (2)求二面角E­BF­C的正弦值．

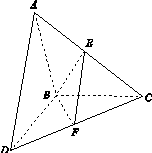
    图1­5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图J11­2①所示，四边形ABCD为等腰梯形，AE⊥DC，AB＝AE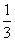＝DC，F为EC的中点．现将△DAE沿AE翻折到△PAE的位置，如图J11­2②所示，且平面PAE⊥平面ABCE.

    (1)求证：平面PAF⊥平面PBE；

    (2)求三棱锥A­PBC与三棱锥E­BPF的体积之比．

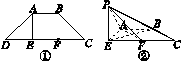
    图J11­2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    .某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．

    (1)求图中x的值；

    (2)从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上(含90分)的人数记为X，求X的分布列与数学期望．

    查看答案和解析>>

    同步练习册答案