
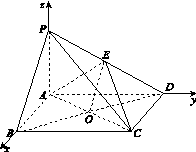
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
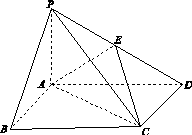
图13
解:(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
因为EO⊂平面AEC,PB⊄平面AEC,
所以PB∥平面AEC.
(2)因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直.
如图,以A为坐标原点, ,AD,AP的方向为x轴、y轴、z轴的正方向,|
,AD,AP的方向为x轴、y轴、z轴的正方向,| |为单位长,建立空间直角坐标系Axyz,则D
|为单位长,建立空间直角坐标系Axyz,则D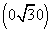 ,E
,E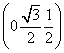 ,
,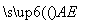 =
=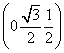 .
.
设B(m,0,0)(m>0),则C(m, ,0),
,0),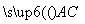 =(m,
=(m, ,0).
,0).
设n1=(x,y,z)为平面ACE的法向量,
则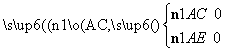 即
即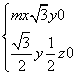
可取n1=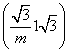 .
.
又n2=(1,0,0)为平面DAE的法向量,
由题设易知|cos〈n1,n2〉|= ,即
,即
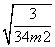 =
= ,解得m=
,解得m=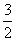 .
.
因为E为PD的中点,所以三棱锥EACD的高为 .三棱锥EACD的体积V=
.三棱锥EACD的体积V=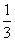 ×
× ×
× ×
×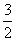 ×
× =
=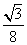 .
.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
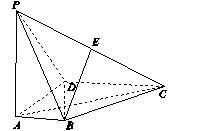
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
一块石材表示的几何体的三视图如图12所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
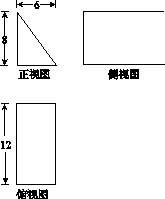
图12
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16所示,四棱柱ABCD A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
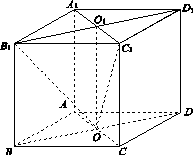
图16
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
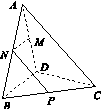
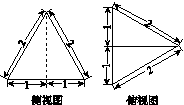
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
下面说法正确的是( )
A. 命题“∃x∈R,使得x2+x+1≥0”的否定是“∀x∈R,使得x2+x+1≥0”
B. 实数x>y是x2>y2成立的充要条件
C. 设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题
D. 命题“若cosα≠1,则α≠0”的逆否命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com