
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
8名世界网球顶级选手在上海大师赛上分成两组,每组各4人,分别进行单循环赛,每组决出前两名,再由每组的第一名与另一组的第二名进行淘汰赛,获胜者角逐冠、亚军,败者角逐第3,4名,大师赛共有________场比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面区域D1={(x,y)|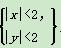 ,D2={(x,y)|(x-2)2+(y-2)2<4}.在区域D1内随机选取一点P,则点P恰好取自区域D2的概率是( )
,D2={(x,y)|(x-2)2+(y-2)2<4}.在区域D1内随机选取一点P,则点P恰好取自区域D2的概率是( )
A.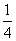 B.
B.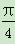
C.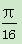 D.
D.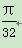
查看答案和解析>>
科目:高中数学 来源: 题型:
国庆节放假,甲去北京旅游的概率为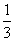 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为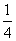 ,
,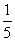 .假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
A. B.
B.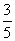
C.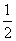 D.
D.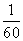
查看答案和解析>>
科目:高中数学 来源: 题型:
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB);
(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
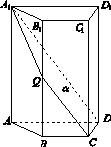
图15
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
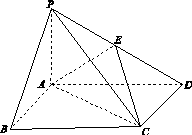
图13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com