
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
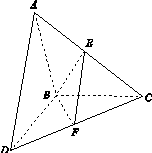
图15
解:(1)证明:方法一,过点E作EO⊥BC,垂足为O,连接OF.由△ABC≌△DBC可证出△EOC≌△FOC,所以∠EOC=∠FOC=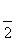 ,即FO⊥BC.又EO⊥BC,EO∩FO=O,所以BC⊥平面EFO.又EF⊂平面EFO,所以EF⊥BC.
,即FO⊥BC.又EO⊥BC,EO∩FO=O,所以BC⊥平面EFO.又EF⊂平面EFO,所以EF⊥BC.

图1
方法二,由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线,并将其作为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线,并将其作为z轴,建立如图所示的空间直角坐标系,易得B(0,0,0),A(0,-1, ),D(
),D( ,-1,0),C(0,2,0),因而E(0,
,-1,0),C(0,2,0),因而E(0, ,
, ),F(
),F( ,
, ,0),所以
,0),所以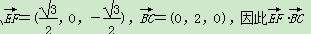 =0,
=0,
从而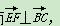 ,所以EF⊥BC.
,所以EF⊥BC.
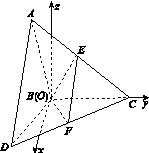
图2
(2)方法一,在图1中,过点O作OG⊥BF,垂足为G,连接EG.因为平面ABC⊥平面BDC,所以EO⊥面BDC,又OG⊥BF,所以由三垂线定理知EG⊥BF,
因此∠EGO为二面角EBFC的平面角.
在△EOC中,EO= EC=
EC= BC·cos 30°=
BC·cos 30°= .
.
由△BGO∽△BFC知,OG=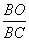 ·FC=
·FC=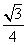 ,因此tan∠EGO=
,因此tan∠EGO=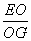 =2,从而得sin∠EGO=
=2,从而得sin∠EGO=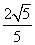 ,即二面角EBFC的正弦值为
,即二面角EBFC的正弦值为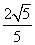 .
.
方法二,在图2中,平面BFC的一个法向量为n1=(0,0,1).
设平面BEF的法向量n2=(x,y,z),
又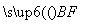 =(
=( ,
, ,0),
,0),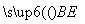 =(0,
=(0, ,
, ),
),
所以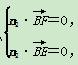 得其中一个n2=(1,-
得其中一个n2=(1,- ,1).
,1).
设二面角EBFC的大小为θ,且由题知θ为锐角,则cos θ=|cos〈n1,n2〉|=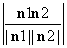 =
=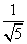 ,
,
因此sin θ= =
=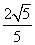 ,即所求二面角正弦值为
,即所求二面角正弦值为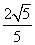 .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
一个口袋中有5个白色乒乓球和5个黄色乒乓球(乒乓球除颜色不同外其他均相同),从中任取5次,每次取出1个后又放回,则抽取的5次中恰有3次取到白球的概率是( )
A.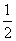 B.
B.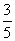
C.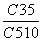 D.C
D.C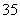 ·0.55
·0.55
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ.
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
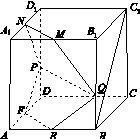
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
一块石材表示的几何体的三视图如图12所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
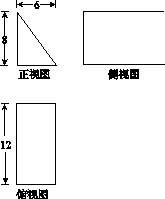
图12
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
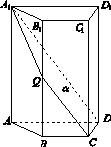
图15
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
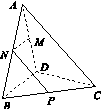
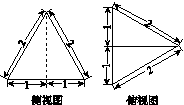
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
如图12,在正方体ABCD A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是( )

图12
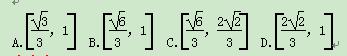
查看答案和解析>>
科目:高中数学 来源: 题型:
中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
|
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 |
| 男生 | 800 | 440 | 200 |
| 女生 | 200 | 160 | 200 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知“跟从别人闯红灯”的人中抽取50人,求n的值.
(2)在“带头闯红灯”的人中,将男生的200人编号为001,002,…,200;将女生的200人编号为201,202,…,400,用系统抽样的方法抽取5人参加“文明交通”宣传活动,若抽取的第一个人的编号为30,把抽取的5人看成一个总体,从这5人中任选取2人,求至少有一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com