
中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
|
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 |
| 男生 | 800 | 440 | 200 |
| 女生 | 200 | 160 | 200 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知“跟从别人闯红灯”的人中抽取50人,求n的值.
(2)在“带头闯红灯”的人中,将男生的200人编号为001,002,…,200;将女生的200人编号为201,202,…,400,用系统抽样的方法抽取5人参加“文明交通”宣传活动,若抽取的第一个人的编号为30,把抽取的5人看成一个总体,从这5人中任选取2人,求至少有一名女生的概率.
解 (1)由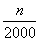 =
=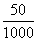 得n=100.
得n=100.
(2)按系统抽样,分段间隔k=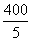 =80.
=80.
当抽取的第一个人的编号为30时,则所抽取的5个人的编号依次为:30,110,190,270,350.
所以抽取的5人中有3男2女.记三个男生分别为A1,A2,A3,两个女生分别为B1,B2,则有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)共有10种情况,其中无女生的情况有(A1,A2),(A1,A3),(A2,A3)3种情况.
记“至少有一名女生”为事件A,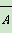 表示“无女生”,P(
表示“无女生”,P(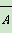 )=
)= ,所以P(A)=1-P(
,所以P(A)=1-P(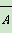 )=
)=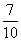 .
.


科目:高中数学 来源: 题型:
如图15所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
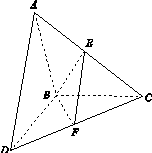
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图J112①所示,四边形ABCD为等腰梯形,AE⊥DC,AB=AE=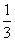 DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
DC,F为EC的中点.现将△DAE沿AE翻折到△PAE的位置,如图J112②所示,且平面PAE⊥平面ABCE.
(1)求证:平面PAF⊥平面PBE;
(2)求三棱锥APBC与三棱锥EBPF的体积之比.
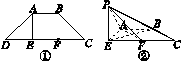
图J112
查看答案和解析>>
科目:高中数学 来源: 题型:
盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
.某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
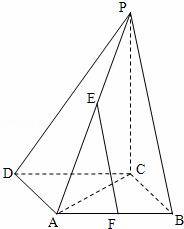
如图,在边长为a的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,E,F是PA和AB的中点.
(1)求证:EF∥平面PBC;
(2)求E到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com