
如图16所示,四棱柱ABCD A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
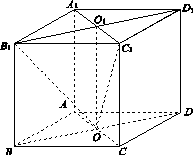
图16
解:(1)如图(a),因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD.
因为CC1∥DD1,所以CC1⊥BD.而AC∩BD=O,因此CC1⊥底面ABCD.
由题设知,O1O∥C1C.故O1O⊥底面ABCD.
(2)方法一: 如图(a),过O1作O1H⊥OB1于H,连接HC1.
由(1)知,O1O⊥底面ABCD,所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.
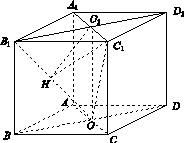
图(a)
又因为四棱柱ABCD A1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形,
因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1.
进而OB1⊥C1H.故∠C1HO1是二面角C1OB1D的平面角.
不妨设AB=2.因为∠CBA=60°,所以OB= ,OC=1,OB1=
,OC=1,OB1=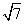 .
.
在Rt△OO1B1中,易知O1H=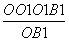 =2
=2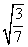 .而O1C1=1,于是C1H=
.而O1C1=1,于是C1H=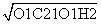 =
=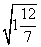 =
=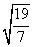 .
.
故cos∠C1HO1=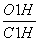 =
=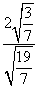 =
=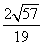 .
.
即二面角C1OB1D的余弦值为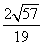 .
.
方法二:因为四棱柱ABCD A1B1C1D1的所有棱长都相等,所以四边形ABCD是菱形,因此AC⊥BD.又O1O⊥底面ABCD,从而OB,OC,OO1两两垂直.
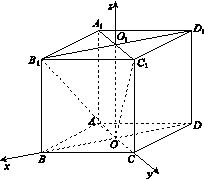
图(b)
如图(b),以O为坐标原点,OB,OC,OO1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系O xyz,不妨设AB=2.因为∠CBA=60°,所以OB= ,OC=1,于是相关各点的坐标为O(0,0,0),
,OC=1,于是相关各点的坐标为O(0,0,0),
B1( ,0,2),C1(0,1,2).
,0,2),C1(0,1,2).
易知,n1=(0,1,0)是平面BDD1B1的一个法向量.
设n2=(x,y,z)是平面OB1C1的一个法向量,则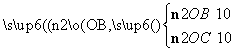 即
即
取z=- ,则x=2,y=2
,则x=2,y=2 ,所以n2=(2,2
,所以n2=(2,2 ,-
,- ).
).
设二面角C1OB1D的大小为θ,易知θ是锐角,于是
cos θ=|cos〈n1,n2〉|=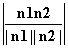 =
=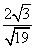 =
=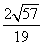 .
.
故二面角C1OB1D的余弦值为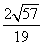 .
.


科目:高中数学 来源: 题型:
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
其中健康指数的含义是:2表示“健康”,1表示“基本健康”,0表示“不健康,但生活能够自理”,-1表示“生活不能自理”.
(1)估计该地区80岁以下老龄人生活能够自理的概率;
(2)若一个地区老龄人健康指数的平均值不小于1.2,则该地区可被评为“老龄健康地区”.请写出该地区老龄人健康指数X的分布列,并判断该地区能否被评为“老龄健康地区”.
查看答案和解析>>
科目:高中数学 来源: 题型:
某高校进行自主招生面试时的程序如下:共设3道题,每道题答对给10分,答错倒扣5分(每道题都必须回答,但相互不影响).设某学生对每道题答对的概率为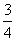 ,则该学生在面试时得分的期望为________.
,则该学生在面试时得分的期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ.
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
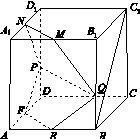
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
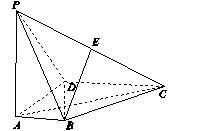
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
一块石材表示的几何体的三视图如图12所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
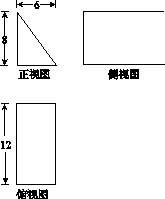
图12
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
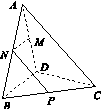
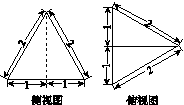
图14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com