
已知命题 :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题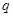 :
:
 恒成立;若
恒成立;若 或
或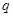 为真,
为真, 且
且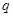 为假,求实数
为假,求实数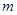 的取值范围.
的取值范围.
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
已知命题 表示双曲线,命题
表示双曲线,命题 表示椭圆.
表示椭圆.
⑴若命题 为真命题,求实数
为真命题,求实数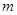 的取值范围.
的取值范围.
⑵判断命题 为真命题是命题
为真命题是命题 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com