Question

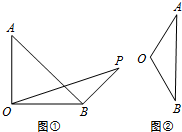
12．在△AOB中，OA=OB=2，
（1）如图①：若AO⊥OB，点P为△AOB所在平面上的一个动点，且满足PO=3，求$\overrightarrow{PB}$•$\overrightarrow{OA}$的取值范围；
（2）如图②：若|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≤$\frac{\sqrt{3}}{3}$|$\overrightarrow{AB}$|，求$\overrightarrow{OA}$与$\overrightarrow{OB}$所成夹角的取值范围．

Answer 1

分析 （1）$\overrightarrow{PB}•\overrightarrow{OA}=（{\overrightarrow{PO}+\overrightarrow{OB}}）•\overrightarrow{OA}=\overrightarrow{PO}•\overrightarrow{OA}+\overrightarrow{OB}•\overrightarrow{OA}$，再根据条件知$\overrightarrow{OB}•\overrightarrow{OA}=0$，即$\overrightarrow{PB}•\overrightarrow{OA}=\overrightarrow{PO}•\overrightarrow{OA}+\overrightarrow{OB}•\overrightarrow{OA}=3×2×cos＜\overrightarrow{PO}，\overrightarrow{OA}＞$，
而$＜\overrightarrow{PO}，\overrightarrow{OA}＞∈[{0，π}]$，很容易算出$\overrightarrow{PB}$•$\overrightarrow{OA}$的取值范围；
（2）过点O作直线AB的垂线，垂足为C，则垂足C必为线段AB的中点，再根据条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≤$\frac{\sqrt{3}}{3}$|$\overrightarrow{AB}$|，得$|{\overrightarrow{OC}}|≤1$，而在RT△OCB中，cos∠$BOC=\frac{OC}{OA}≤\frac{1}{2}$，
∠$BOC∈[{\frac{π}{3}，\frac{π}{2}}）$，又∠AOB=2∠BOC，则∠$AOB∈[{\frac{2π}{3}，π}）$，即$\overrightarrow{OA}$与$\overrightarrow{OB}$所成夹角的取值范围为$[{\frac{2π}{3}，π}）$．

解答 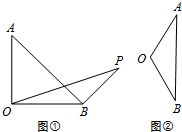（本小题满分16分）
解：（1）∵$\overrightarrow{PB}=\overrightarrow{PO}+\overrightarrow{OB}$，
∴$\overrightarrow{PB}•\overrightarrow{OA}=（{\overrightarrow{PO}+\overrightarrow{OB}}）•\overrightarrow{OA}=\overrightarrow{PO}•\overrightarrow{OA}+\overrightarrow{OB}•\overrightarrow{OA}$…（2分）
又∵在△AOB中，OA=OB=2，PO=3，AO⊥OB
∴$\overrightarrow{OB}•\overrightarrow{OA}=0$，且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=2$，$|{\overrightarrow{PO}}|=3$，…（4分）
即$\overrightarrow{PB}•\overrightarrow{OA}=\overrightarrow{PO}•\overrightarrow{OA}+\overrightarrow{OB}•\overrightarrow{OA}=3×2×cos＜\overrightarrow{PO}，\overrightarrow{OA}＞$，
当点P在△AOB所在平面上运动时，则$＜\overrightarrow{PO}，\overrightarrow{OA}＞∈[{0，π}]$，…（6分）
即$6cos＜\overrightarrow{PO}，\overrightarrow{ON}＞∈[{-6，6}]$，
也即所求$\overrightarrow{PB}$•$\overrightarrow{OA}$的取值范围为[-6，6]…（8分）
（2）过点O作直线AB的垂线，垂足为C，
则垂足C必为线段AB的中点，
且$|{\overrightarrow{OA}+\overrightarrow{OB}}|=|{2\overrightarrow{OC}}|=2|{\overrightarrow{OC}}|$，…（10分）
又在RT△OCB中，$|{\overrightarrow{AB}}|=2|{\overrightarrow{CB}}|=2\sqrt{{2^2}-{{|{\overrightarrow{OC}}|}^2}}$，
又∵$|{\overrightarrow{OA}+\overrightarrow{OB}}|≤\frac{{\sqrt{3}}}{3}|{\overrightarrow{AB}}|$，∴$2|{\overrightarrow{OC}}|≤\frac{{\sqrt{3}}}{3}×$$2\sqrt{{2^2}-{{|{\overrightarrow{OC}}|}^2}}$，
即$|{\overrightarrow{OC}}|≤1$，…（12分）
在RT△OCB中，∵cos∠$BOC=\frac{OC}{OA}≤\frac{1}{2}$，∴∠$BOC∈[{\frac{π}{3}，\frac{π}{2}}）$，…（14分）
又∠AOB=2∠BOC，则∠$AOB∈[{\frac{2π}{3}，π}）$，
即$\overrightarrow{OA}$与$\overrightarrow{OB}$所成夹角的取值范围为$[{\frac{2π}{3}，π}）$…（16分）

点评 本题考查了平面向量在三角形中的应用，对学生综合应用知识的能力有较高要求，属于中档题．