
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
分析 根据方差抽样的定义即可求应从各年级分别抽取的班数,根据古典概型的概率公式即可求出对应的概率.
解答 解:∵高一,高二,高三的班级数比为21:14:7=3:2:1,
则现采用分层抽样的方法从这些班中抽取6个班,则高一,高二,高三的班数分别为3,2,1.分别
若从抽取的6个班高三班级记为a,高二的两个班级记为b,c,高一的三个班级记为A,B,C,
则抽取2人的结果是(a,b),(a,c),(a,A),(a,B),(a,C),(b,c),(b,A),(b,B),(b,C),(c,A),(c,B),(c,C),
(A,B),(A,C),(B,C),共15种结果.
抽取的2人均为高一班级(A,B),(A,C),(B,C),共3种结果.
则抽取的2个班均为高一的概率是P=$\frac{3}{15}$=$\frac{1}{5}$,
故选:A.
点评 本题主要考查分层抽样的应用以及古典概率的计算,利用列举法是解决本题概型的基本方法.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
| 日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x(℃) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
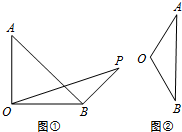 在△AOB中,OA=OB=2,
在△AOB中,OA=OB=2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
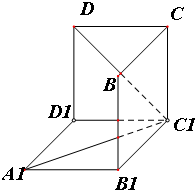 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B. | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com