
分析 (1)A,B,C三点共线,可得kAB=kAC,即可得出.
(2)由直线CD⊥AB,且BC∥AD.可得kAB•kCD=-1,kBC=kAD.
解答 解:(1)kAB=$\frac{2-0}{1-(-1)}$=1,kAC=$\frac{2-a}{1-3}$=$\frac{a-2}{2}$.∵A,B,C三点共线,∴kAB=kAC,
∴$\frac{a-2}{2}$=1,解得a=4.
(2)设D(x,y),kAB=$\frac{-1-2}{1-2}$=3,kCD=$\frac{y-0}{x-3}$=$\frac{y}{x-3}$,kBC=$\frac{2-0}{2-3}$=-2,kAD=$\frac{y+1}{x-1}$.
∵直线CD⊥AB,且BC∥AD.
∴kAB•kCD=3•$\frac{y}{x-3}$=-1,kBC=kAD,即$\frac{y+1}{x-1}$=-2.
联立解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,即D(0,1).
点评 本题考查了直线斜率计算公式、相互垂直与相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
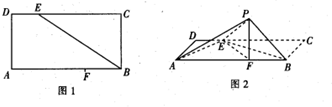 如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.
如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com