
平面直角坐标系xoy中,动点 满足:点P到定点
满足:点P到定点 与到y轴的距离之差为
与到y轴的距离之差为 .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C.
(1)求曲线C的轨迹方程;
(2)过点F的直线交曲线C于A、B两点,过点A和原点O的直线交直线 于点D,求证:直线DB平行于x轴.
于点D,求证:直线DB平行于x轴.
(1)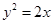 ,(2)详见解析.
,(2)详见解析.
解析试题分析:(1)求动点轨迹方程,首先设动点坐标,本题已设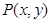 ,其次列动点满足条件
,其次列动点满足条件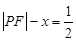 ,然后利用坐标化简关系式,即
,然后利用坐标化简关系式,即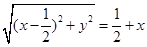 ,
,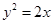 ,最后要考虑动点满足限制条件,本题为已知条件
,最后要考虑动点满足限制条件,本题为已知条件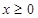 ,另外本题对条件
,另外本题对条件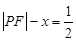 的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于
的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于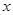 轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设
轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设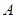 的坐标为
的坐标为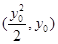 ,利用
,利用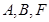 三点共线解出点
三点共线解出点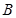 的纵坐标为
的纵坐标为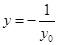 ,根据直线
,根据直线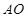 与直线
与直线 的交点解出
的交点解出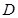 的纵坐标也为
的纵坐标也为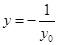 .
.
试题解析:(1)依题意: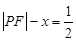 2分
2分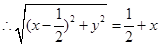
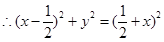 4分
4分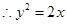 6分
6分
注:或直接用定义求解.
(2)法1:设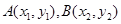 ,直线
,直线 的方程为
的方程为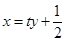
由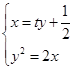 得
得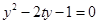 8分
8分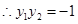
直线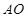 的方程为
的方程为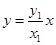
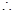 点
点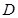 的坐标为
的坐标为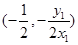 2分
2分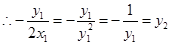
 直线
直线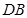 平行于
平行于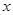 轴. 14分
轴. 14分
法2:设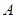 的坐标为
的坐标为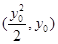 ,则
,则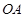 的方程为
的方程为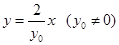
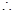 点
点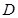 的纵坐标为
的纵坐标为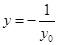 , 8分
, 8分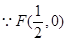
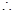 直线
直线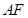 的方程为
的方程为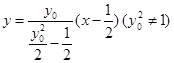
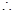 点
点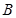 的纵坐标为
的纵坐标为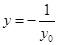 . 12分
. 12分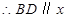 轴;当
轴;当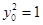 时,结论也成立,
时,结论也成立,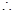 直线
直线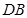 平行于
平行于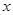 轴. 14分
轴. 14分
考点:轨迹方程,直线与抛物线位置关系


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为 和
和 ,且|
,且|
 |=2,
|=2,
点(1,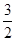 )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP0,垂足为P0,且 =
=
 .
.
(1)求点M的轨迹C的方程;
(2)设直线l:y=kx+m(m≠0)与(1)中的轨迹C交于不同的两点A,B.
若直线OA,AB,OB的斜率成等比数列,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆C与两圆x2+(y+4)2=1,x2+(y-2)2=1外切,圆C的圆心轨迹方程为L,设L上的点与点M(x,y)的距离的最小值为m,点F(0,1)与点M(x,y)的距离为n.
(1)求圆C的圆心轨迹L的方程.
(2)求满足条件m=n的点M的轨迹Q的方程.
(3)在(2)的条件下,试探究轨迹Q上是否存在点B(x1,y1),使得过点B的切线与两坐标轴围成的三角形的面积等于 .若存在,请求出点B的坐标;若不存在,请说明理由.
.若存在,请求出点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 :
: 的离心率为
的离心率为 ,右焦点
,右焦点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆右焦点F2斜率为 (
( )的直线
)的直线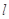 与椭圆
与椭圆 相交于
相交于 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段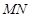 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点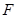 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为 (
( 为常数且
为常数且 ).
).
(1)求 的值;
的值;
(2) 为抛物线的顶点,
为抛物线的顶点, ,
, ,
, 的面积分别记为
的面积分别记为 ,
, ,
,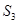 ,求证:
,求证: 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足 +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当|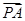 -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com