
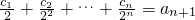 成立,求c1+c2+…+c2012的值.
成立,求c1+c2+…+c2012的值.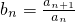 (n∈N*),求证:数列{bn}中的任意一项总可以表示成其他两项之积.
(n∈N*),求证:数列{bn}中的任意一项总可以表示成其他两项之积.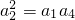 …(2分)
…(2分)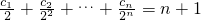 对n∈N*都成立,
对n∈N*都成立,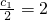 ,得c1=4,…(5分)
,得c1=4,…(5分)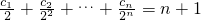 ,①
,①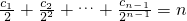 ,②
,②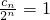 ,得
,得 …(7分)
…(7分)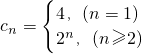 .…(8分)
.…(8分)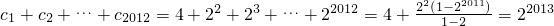 …(10分)
…(10分)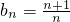 ,只需
,只需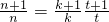 ,…(12分)
,…(12分)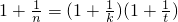 ,即
,即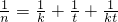
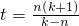 取k=n+1,则t=n(n+2)…(14分)
取k=n+1,则t=n(n+2)…(14分)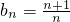 ,
,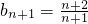 和
和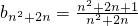 ,
,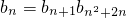 .…(16分)
.…(16分)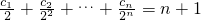 对n∈N*都成立,能推导出
对n∈N*都成立,能推导出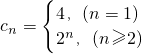 ,由此能求出c1+c2+…+c2012的值.
,由此能求出c1+c2+…+c2012的值.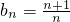 ,只需
,只需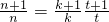 ,由此能够证明数列{bn}中的任意一项总可以表示成其他两项之积.
,由此能够证明数列{bn}中的任意一项总可以表示成其他两项之积.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
| an+1 | Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•松江区一模)已知递增的等差数列{an}的首项a1=1,且a1、a2、a4成等比数列.
(2013•松江区一模)已知递增的等差数列{an}的首项a1=1,且a1、a2、a4成等比数列.| c1 |
| 2 |
| c2 |
| 22 |
| cn |
| 2n |
| dn |
| dn+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com