
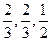 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:不详 题型:解答题
| 日销售量 | 天数 | 概率 |
| 25瓶 | 20 | 0.10 |
| 26瓶 | 60 | 0.30 |
| 27瓶 | 100 | 0.50 |
| 28瓶 | 20 | 0.10 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 相关人员数 | 抽取人数 |
| 公务员 | 32 |  |
| 教师 | 48 |  |
| 自由职业者 | 64 | 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.至少有1枚正面和最多有1枚正面 |
| B.最多1枚正面和恰有2枚正面 |
| C.至多1枚正面和至少有2枚正面 |
| D.至少有2枚正面和恰有1枚正面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑里的种子都没发芽,则这个坑需要补种,假定每个坑至多补种一次,每补种1个坑需10元,用
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑里的种子都没发芽,则这个坑需要补种,假定每个坑至多补种一次,每补种1个坑需10元,用 表示补种费用,则
表示补种费用,则 的数学期望为
的数学期望为| A.10元 | B.20元 | C.40元 | D.80元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com