
【题目】(本题满分12分)已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() 为椭圆
为椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于
![]() 的动点,直线
的动点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点.证明:
两点.证明:![]() 恒为定值.
恒为定值.
【答案】(Ⅰ)![]() . (Ⅱ)
. (Ⅱ)![]() 为定值
为定值![]() .证明见解析。
.证明见解析。
【解析】本试题主要是考出了椭圆方程的求解,椭圆的几何性质,直线与椭圆的位置关系的运用的综合考查,体现了运用代数的方法解决解析几何的本质的运用。
(1)首先根据题意的几何性质来表示得到关于a,b,c的关系式,从而得到其椭圆的方程。
(2设出直线方程,设点P的坐标,点斜式得到AP的方程,然后联立方程组,可知借助于韦达定理表示出长度,进而证明为定值。
(Ⅰ)解:由题意可知,![]() ,
,![]() ,
,
解得![]() . …………4分
. …………4分
所以椭圆的方程为![]() . …………5分
. …………5分
(Ⅱ)证明:由(Ⅰ)可知,![]() ,
,![]() .设
.设![]() ,依题意
,依题意![]() ,
,
于是直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则![]() .
.
即![]() . …………7分
. …………7分
又直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则![]() ,
,
即![]() . …………9分
. …………9分
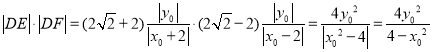 …………11分
…………11分
又![]() 在
在![]() 上,所以
上,所以![]() ,即
,即![]() ,代入上式,
,代入上式,
得![]() ,所以
,所以![]() 为定值
为定值![]() . …………12分
. …………12分


科目:高中数学 来源: 题型:
【题目】为迎接![]() 月
月![]() 日的“全民健身日”,某大学学生会从全体男生中随机抽取
日的“全民健身日”,某大学学生会从全体男生中随机抽取![]() 名男生参加
名男生参加![]() 米中长跑测试,经测试得到每个男生的跑步所用时间的茎叶图(小数点前一位数字为茎,小数点的后一位数字为叶),如图,若跑步时间不高于
米中长跑测试,经测试得到每个男生的跑步所用时间的茎叶图(小数点前一位数字为茎,小数点的后一位数字为叶),如图,若跑步时间不高于![]() 秒,则称为“好体能”.
秒,则称为“好体能”.
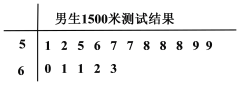
(Ⅰ) 写出这组数据的众数和中位数;
(Ⅱ)要从这 ![]() 人中随机选取
人中随机选取![]() 人,求至少有
人,求至少有![]() 人是“好体能”的概率;
人是“好体能”的概率;
(Ⅲ)以这 ![]() 人的样本数据来估计整个学校男生的总体数据,若从该校男生(人数众多)任取
人的样本数据来估计整个学校男生的总体数据,若从该校男生(人数众多)任取![]() 人,记
人,记![]() 表示抽到“好体能”学生的人数,求
表示抽到“好体能”学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在
在![]() 轴的正半轴上,半径为2,且被直线
轴的正半轴上,半径为2,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,证明:经过
,证明:经过![]() ,
,![]() ,
,![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数.①若存在
上的函数.①若存在![]() ,使
,使![]() 成立,则函数
成立,则函数![]() 在
在![]() 上单调递增;②若存在
上单调递增;②若存在![]() ,使
,使![]() 成立,则函数
成立,则函数![]() 在
在![]() 上不可能单调递减;③若存在
上不可能单调递减;③若存在![]() 对于任意
对于任意![]() 都有
都有![]() 成立,则函数
成立,则函数![]() 在
在![]() 上单调递增.则以上述说法正确的是_________.(填写序号)
上单调递增.则以上述说法正确的是_________.(填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若函数![]() 满足
满足![]() ,则函数
,则函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
②点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ;
;
③通过回归方程![]() 可以估计和观测变量的取值和变化趋势;
可以估计和观测变量的取值和变化趋势;
④正弦函数是奇函数,![]() 是正弦函数,所以
是正弦函数,所以![]() 是奇函数,上述推理错误的原因是大前提不正确.
是奇函数,上述推理错误的原因是大前提不正确.
其中真命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,由以上数据完成下列2×2列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
移动支付活跃用户 | 非移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 | 100 |
(2)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com