
(1)求A、B、C的值;
(2)若顶点C的对边c上的高等于4![]() ,求△ABC各边的长.
,求△ABC各边的长.
思路分析:结合题目的条件,由tanA·tanC=2+![]() ,A+C=2B,可知B=60°,A+C=120°,
,A+C=2B,可知B=60°,A+C=120°,
∴可利用两角和的正切公式求tanA+tanC,从而构造方程求A与C的正切值,再求角A与C.
解:(1)∵A+C=2B,A+C+B=180°,
∴B=60°.∴A+C=120°.
∴tan(A+C)=![]() =-
=-![]() ,
,
则tanA+tanC=3+![]() .
.
那么tanA、tanC即为x2-(3+![]() )x+(2+
)x+(2+![]() )=0的两根.
)=0的两根.
∴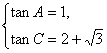 或
或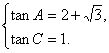
∴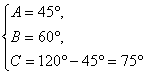 或
或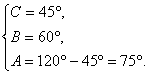
(2)如图,当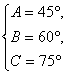 时,
时,
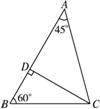
∵CD=4![]() ,∴CB=8,BD=4,AD=4
,∴CB=8,BD=4,AD=4![]() ,AC=4
,AC=4![]() .
.
∴AB=4+4![]() .
.
当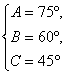 时,如图.
时,如图.
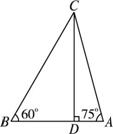
∵CD=4![]() ,∴CB=8,BD=4,
,∴CB=8,BD=4,
AC=![]() =
=![]() =
=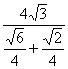 =
=![]()
=4![]() (
(![]() -
-![]() )=4
)=4![]() (
(![]() -1).
-1).
∴AB=BD+AD=4+4![]() (2-
(2-![]() )=8
)=8![]() -8.
-8.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com