
����Ŀ��ij��ҵ����Ա��10000�ˣ���ͼ��ͨ����������õ��ĸ���ҵ����Ա�������루��λ����Ԫ��Ƶ�ʷֲ�ֱ��ͼ.
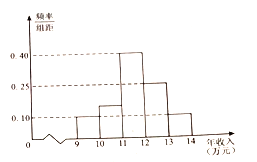
��1������Ƶ�ʷֲ�ֱ��ͼ����������ƽ����.���Դ˹������ҵȫ��Ա���������벻��������ƽ������������ͬһ���е����������������������е��ֵ����������
��2��������������������![]() ��ԪԱ����2�ˣ�����������
��ԪԱ����2�ˣ�����������![]() ��Ԫ��Ա������ȡ3�ˣ�ǡ��2λԱ��������
��Ԫ��Ա������ȡ3�ˣ�ǡ��2λԱ��������![]() ��Ԫ�ĸ��ʣ�
��Ԫ�ĸ��ʣ�
��3�����������������������400�ˣ�����400���У���������![]() ��Ԫ��Ա���о��д�ѧ����ѧ����ѧ������
��Ԫ��Ա���о��д�ѧ����ѧ����ѧ������![]() ����������
����������![]() ��Ԫ��Ա���в����д�ѧ����ѧ����ѧ������
��Ԫ��Ա���в����д�ѧ����ѧ����ѧ������![]() �������д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա��������������������������ж��ܷ���
�������д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա��������������������������ж��ܷ���![]() �İ�����Ϊ���д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա�������в��죿
�İ�����Ϊ���д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա�������в��죿
���д�ѧ����ѧ����ѧ�� | �����д�ѧ����ѧ����ѧ�� | �ϼ� | |
| |||
| |||
�ϼ� |
����![]() ��
��
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1��5100�ˣ�2��![]() ��3��������
��3��������
��������
����Ƶ�ʷֲ�ֱ��ͼ�õ�ÿ�����������Ӧ��Ƶ�ʣ�
(1)��������ƽ����![]() ����ÿ�����������е��ֵ�����Ƶ�ʳ˻��ĺͣ�����Ƶ�ʷֲ�ֱ��ͼ���ɵõ������벻����ƽ������Ƶ�ʣ������ɵö�Ӧ������
����ÿ�����������е��ֵ�����Ƶ�ʳ˻��ĺͣ�����Ƶ�ʷֲ�ֱ��ͼ���ɵõ������벻����ƽ������Ƶ�ʣ������ɵö�Ӧ������
(2)���оٷ��ֱ�д����![]() ��Ԫ��Ա������ȡ3�˺�ǡ��2λԱ��������
��Ԫ��Ա������ȡ3�˺�ǡ��2λԱ��������![]() ��Ԫ�������Ļ����¼������ɵó����.
��Ԫ�������Ļ����¼������ɵó����.
(3)������������������������������![]() �������
�������![]() �Ĺ۲�ֵk,��Ӧ�������������ж�.
�Ĺ۲�ֵk,��Ӧ�������������ж�.
��Ƶ�ʷֲ�ֱ��ͼ������������Ƶ�ʶ�Ӧ���±�
�������� |
|
|
|
|
|
Ƶ�� | 0.10 | 0.15 | 0.40 | 0.25 | 0.10 |
��1������ͳ�Ʒ����У�ͬһ�������ø���������е�ֵ��Ϊ����.��������ƽ����![]()
![]() ����Ԫ��
����Ԫ��
��Ƶ�ʷֲ�ֱ��ͼ�ij����ã������벻����ƽ������Ƶ����0.51.�Դ˹��Ƹ���ҵȫ��Ա���������벻����ƽ������Ƶ����0.51.����ҵ������������������Լ��![]() ��
��
��2������������������Ƶ�ʷֲ���Ӧ������ã�����![]() ��2�ˣ��ֱ����2��Ϊ�ס��ң�����ô��
��2�ˣ��ֱ����2��Ϊ�ס��ң�����ô��![]() ����3�ˣ��ֱ����3��Ϊ
����3�ˣ��ֱ����3��Ϊ![]() ��
��![]() ��
��![]() ����������
����������![]() ��5��.
��5��.
|
|
|
|
| |
1 | �� | �� | �� | ||
2 | �� | �� | �� | ||
3 | �� | �� | �� | ||
4 | �� | �� | �� | ||
5 | �� | �� | �� | ||
6 | �� | �� | �� | ||
7 | �� | �� | �� | ||
8 | �� | �� | �� | ||
9 | �� | �� | �� | ||
10 | �� | �� | �� |
�ɱ�֪����������![]() ��5���������ȡ3�˹���10�ֳ鷨������ǡ��2λԱ��������
��5���������ȡ3�˹���10�ֳ鷨������ǡ��2λԱ��������![]() �鷨����6��
�鷨����6��
���������![]()
��3����������Ϊ400��ʱ��������������Ƶ�ʶ�Ӧ��֪����������![]() ��
��![]() �ڶ���40��.����֪���������
�ڶ���40��.����֪���������![]() ������
������
���д�ѧ����ѧ����ѧ�� | �����д�ѧ����ѧ����ѧ�� | �ϼ� | |
| 16 | 24 | 40 |
| 28 | 12 | 40 |
�ϼ� | 44 | 36 | 80 |
![]()
![]()
��![]() �İ�����Ϊ���д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա�������в���
�İ�����Ϊ���д�ѧ����ѧ����ѧ���Ͳ����д�ѧ����ѧ����ѧ����Ա�������в���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������![]() ���䶨������Ϊ����������
���䶨������Ϊ����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�2���������£��躯��![]() ������
������![]() �����ٴ���һ��
�����ٴ���һ��![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() .
.
��1����![]() ��
��![]() ���м�ֵ�����Ƿ����ʵ��m��ʹ�ò���ʽ
���м�ֵ�����Ƿ����ʵ��m��ʹ�ò���ʽ![]() ������
������![]() ��
��![]() ������������ڣ����m��ȡֵ��Χ���������ڣ���˵������.
������������ڣ����m��ȡֵ��Χ���������ڣ���˵������.![]() ��
��
��2����![]() ����
����![]() .
.
����֤����![]() ʱ��
ʱ��![]() ��
��
����![]() ����֤��
����֤��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() �͵�
�͵�![]() .
.
��1������![]() ��Բ
��Բ![]() �����ߣ������ߵķ��̣�
�����ߣ������ߵķ��̣�
��2�����Ե�![]() ΪԲ�ģ��ұ�ֱ��
ΪԲ�ģ��ұ�ֱ��![]() �صõ��ҳ�Ϊ8��Բ
�صõ��ҳ�Ϊ8��Բ![]() �ķ��̣�
�ķ��̣�
��3����![]() Ϊ��2����Բ
Ϊ��2����Բ![]() ������һ�㣬����
������һ�㣬����![]() ��Բ
��Բ![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ����̽����ƽ�����Ƿ����һ����
����̽����ƽ�����Ƿ����һ����![]() ��ʹ��
��ʹ��![]() Ϊ��ֵ�������ڣ����������
Ϊ��ֵ�������ڣ����������![]() �����꣬��ָ����Ӧ�Ķ�ֵ���������ڣ���˵������.
�����꣬��ָ����Ӧ�Ķ�ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������Ա����������9����һֱ�Ը���ɽ����ֳҵ�Ĺ�ģ���и��ٵ��飬�����ṩ�˸���ijɽ����ֳ������ֳ����![]() ����λ����ֻ������Ӧ���
����λ����ֻ������Ӧ���![]() ����ţ������ݱ���ɢ��ͼ����ͼ��ʾ��������ɢ��ͼ������
����ţ������ݱ���ɢ��ͼ����ͼ��ʾ��������ɢ��ͼ������![]() ��
��![]() �н�ǿ��������ع�ϵ�������ṩ�˸���ɽ����ֳ���ĸ���
�н�ǿ��������ع�ϵ�������ṩ�˸���ɽ����ֳ���ĸ���![]() ����λ����������
����λ����������![]() �Ļع鷽��
�Ļع鷽��![]() .
.
������x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
����ֳɽ��y/��ֻ | 1.2 | 1.5 | 1.6 | 1.6 | 1.8 | 2.5 | 25 | 2.6 | 2.7 |
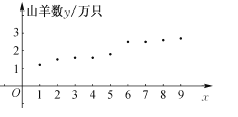
���ݱ��е����ݺ�����ͳ��������![]() ����
����![]() �����Իع鷽�̣��ο�ͳ������
�����Իع鷽�̣��ο�ͳ������![]() ��
��![]() ����
����
��������һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ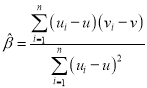 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABC-A1B1C1�У������ABC��ֱ�������Σ�AC=BC=AA1=2��DΪ����AA1���е㣮

��1��������ֱ��DC1��B1C���ɽǵ�����ֵ��
��2��������B1-DC-C1��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��A(0����2)��B(4��0)��ԲC������(0����1)��(0��1)��(![]() ��0)��б��Ϊk��ֱ��l������B��
��0)��б��Ϊk��ֱ��l������B��
��1����ԲC�ı����̣�
��2����k��2ʱ����ֱ��l�ϵ�һ��P��ԲC��һ�����ߣ��е�ΪQ��������PQ��![]() �����P�����ꣻ
�����P�����ꣻ
��3����M��N��ԲC������������ͬ�ĵ㣬����MNΪֱ����Բ��ֱ��l��û�й����㣬��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��ѵԱ��ij��ܣ���ѵ���������ַ�ʽ��
��ʽһ����һ������ÿ����ѵ1Сʱ�����ղ���
��ʽ��������һ����ѵ4Сʱ�����ղ���
��˾�ж�����飬ÿ������60�ˣ�����ѡ����![]() ��Ϊ���顢����
��Ϊ���顢����![]() ����ѵ������ѡ��ʽһ������ѡ��ʽ��������¼ÿ����ѵ����Դ������������
����ѵ������ѡ��ʽһ������ѡ��ʽ��������¼ÿ����ѵ����Դ������������
��һ�� | �ڶ��� | ������ | ������ | |
���� | 20 | 25 | 10 | 5 |
���� | 8 | 16 | 20 | 16 |
![]() �÷�ʽһ�뷽ʽ��������ѵ���ֱ����Ա����ѵ��ƽ��ʱ��
�÷�ʽһ�뷽ʽ��������ѵ���ֱ����Ա����ѵ��ƽ��ʱ��![]() ��ȷ��
��ȷ��![]() �����ݴ��ж�������ѵ��ʽЧ�ʸ��ߣ�
�����ݴ��ж�������ѵ��ʽЧ�ʸ��ߣ�
![]() �ڼ��������У��ӵ�������ѵ�����Ա���в��÷ֲ�����ķ�����ȡ6�ˣ��ٴ���6���������ȡ2�ˣ�����2����������1�����Լ���ĸ��ʣ�
�ڼ��������У��ӵ�������ѵ�����Ա���в��÷ֲ�����ķ�����ȡ6�ˣ��ٴ���6���������ȡ2�ˣ�����2����������1�����Լ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com