
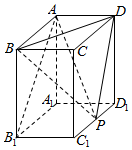
 如图,已知长方体ABCD-A1B1C1D1,底面是边长为1的正方形,高AA1=2.
如图,已知长方体ABCD-A1B1C1D1,底面是边长为1的正方形,高AA1=2.分析 (1)根据异面直线所成角的定义进行求解即可.
(2)根据三棱锥的体积公式进行计算即可.
解答 解:(1)∵BD∥B1D1,AB1=AD1,
∴∠AB1D1(或其补角)为异面直线BD与AB1所成的角,
∵$cos∠A{B_1}{D_1}=\frac{{A{B_1}^2+{B_1}{D_1}^2-A{D_1}^2}}{{2A{B_1}•{B_1}{D_1}}}=\frac{{\sqrt{10}}}{10}$,
∴$异面直线BD与A{B_1}所成的角的余弦值为\frac{{\sqrt{10}}}{10}$.
(2)VP-ABD=$\frac{1}{3}$S△ABD•h=$\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{1}{3}$.
点评 本题主要考查异面直线所成角的求解以及空间三棱锥的体积的计算,根据相应的定义和公式是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
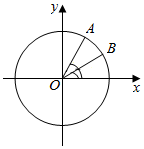 如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 91.5和91.5 | B. | 91.5和92 | C. | 91和91.5 | D. | 92和92 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
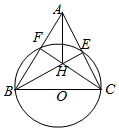 如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:
如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com